Zadanie nr 8210947
Kolejne wyrazy ciągu 1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9... wpisujemy spiralnie w kratki nieskończonego diagramu, tak jak na rysunku obok. Jaką liczbę wpiszemy w setnej kratce ponad kratką zacieniowaną?
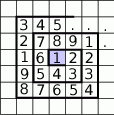
A) 8 B) 5 C) 6 D) 1 E) 3
Rozwiązanie
Zanim ustalimy jaka liczba będzie wpisana w opisanym miejscu, spróbujmy ustalić, który to będzie wyraz ciągu. Jeżeli wyobrazimy sobie jaki będzie obrazek, gdy ostatnim napisanym wyrazem będzie ten w setnej kratce ponad zacieniowaną, to w sumie będzie napisanych
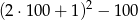
(bo brakuje 100 liczb do pełnego kwadratu o boku 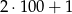 ). Tak naprawdę intersuje nas jaka jest reszta z dzielenia tej liczby przez 9 (bo wyrazy ciągu powtarzają się co 9). Możemy więc zastapić 100 przez resztę z dzielenia przez 9, czyli przez 1.
). Tak naprawdę intersuje nas jaka jest reszta z dzielenia tej liczby przez 9 (bo wyrazy ciągu powtarzają się co 9). Możemy więc zastapić 100 przez resztę z dzielenia przez 9, czyli przez 1.
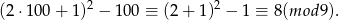
Zatem szukany wyraz będzie taki sam jak wyraz 8, czyli będzie to 8.
Odpowiedź: A

