/Studia/Analiza/Funkcje/Badanie funkcji/Ciągłość

Zadanie nr 6718798

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 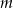m funkcja

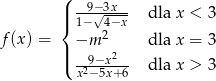
( --9−3x-- ||{ 1− √4−x- dla x < 3 f(x ) = −m 2 dla x = 3 || 9−x2 ( x2−-5x+-6 dla x > 3

jest ciągła w zbiorze liczb rzeczywistych?

Rozwiązanie

Na początek sprawdźmy, kiedy mianowniki podanych funkcji się zerują

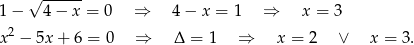
√ ------ 1− 4− x = 0 ⇒ 4 − x = 1 ⇒ x = 3 x2 − 5x+ 6 = 0 ⇒ Δ = 1 ⇒ x = 2 ∨ x = 3.

Jest więc jasne, że dla 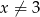x ⁄= 3 , podana funkcja jest ciągła (jest wtedy dana ’porządnym’ wzorem). Jedyny problem to 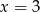x = 3 . Aby funkcja była ciągła dla 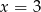x = 3 , wszystkie 3 wzory muszą dawać tę samą wartość dla 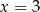x = 3 . Oczywiście w przypadku pierwszego i trzeciego wzoru, nie ma sensu wartość dla 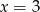x = 3 (bo wtedy mianownik się zeruje), ale ma sens granica w 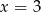x = 3 . Liczymy

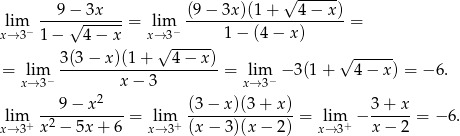
√ ------ 9− 3x (9 − 3x)(1 + 4 − x ) lim− ----√-------= lim− ----------------------= x→3 1 − 4 − x x→√3------ 1 − (4 − x) 3(3 − x)(1 + 4 − x) √ ------ = lim− ----------------------= lim− − 3(1 + 4 − x) = − 6. x→ 3 x − 3 x→ 3 ---9−--x2--- (3-−-x-)(3-+-x-) 3-+-x- lxi→m3+ x2 − 5x + 6 = xli→m3+(x − 3 )(x − 2) = xli→m3+− x − 2 = − 6.

Tak więc funkcja będzie ciągła w 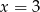x = 3 o ile

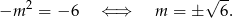
2 √ -- −m = − 6 ⇐ ⇒ m = ± 6.

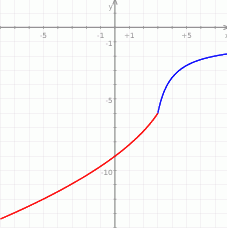
Na koniec, dla ciekawskich, wykres funkcji 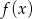f(x) .

PIC

 
Odpowiedź: √ -- m = ± 6

Wersja PDF