/Szkoła średnia/Równania/Z kropkami

Zadanie nr 1784279

Wyznacz te wartości parametru m , dla których równanie

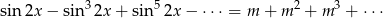
3 5 2 3 sin 2x − sin 2x+ sin 2x − ⋅⋅ ⋅ = m + m + m + ⋅⋅⋅

ma rozwiązania?

Wersja PDF

Rozwiązanie

Lewa strona jest zbieżnym szeregiem geometrycznym o ile 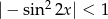2 |− sin 2x| < 1 , czyli dla 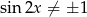sin 2x ⁄= ± 1 . Prawa strona jest natomiast zbieżna, o ile 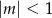|m | < 1 . Mamy wtedy

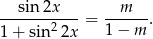
--sin2x----= --m---. 1+ sin 22x 1 − m

Aby ustalić dla jakich wartości parametru 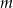m równanie to ma rozwiązanie, spróbujemy sprawdzić jakie wartości przyjmuje lewa strona. Jeżeli podstawimy 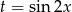t = sin 2x to mamy funkcję

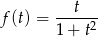
t f (t) = 1+--t2-

na przedziale 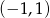(− 1,1) (wartości 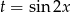t = sin2x ). Policzmy jej pochodną

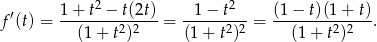
′ 1 + t2 − t(2t) 1− t2 (1 − t)(1 + t) f (t) = --------2-2---= ------2-2 = ---------2-2--. (1+ t) (1 + t ) (1+ t )

Widać, że dla 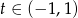t ∈ (− 1,1) pochodna jest dodatnia, czyli 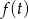f(t) jest rosnąca. Zatem wartości 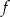f na przedziale 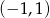(− 1,1) to dokładnie przedział

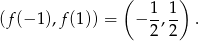
( ) (f (−1 ),f(1)) = − 1, 1- . 2 2

Pozostało ustalić kiedy

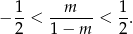
− 1-< --m---< 1-. 2 1− m 2

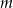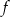Jeżeli ten warunek będzie spełniony, dla odpowiedniego m będzie zawszem można dobrać x , czyli równanie będzie miało rozwiązanie (w dodatku dokładnie jedno, bo f jest rosnąca).

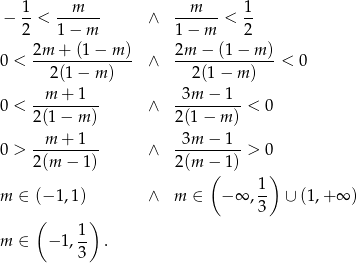
1- --m--- --m--- 1- − 2 < 1 − m ∧ 1 − m < 2 0 < 2m-+--(1−--m-) ∧ 2m--−-(1-−-m-) < 0 2 (1 − m ) 2(1− m ) m + 1 3m − 1 0 < --------- ∧ --------- < 0 2(1 − m ) 2 (1− m) --m-+-1-- -3m--−-1- 0 > 2(m − 1) ∧ 2 (m − 1) > 0 ( ) m ∈ (− 1,1) ∧ m ∈ − ∞ , 1 ∪ (1 ,+∞ ) 3 ( 1 ) m ∈ − 1,-- . 3

 
Odpowiedź: ( ) m ∈ − 1, 13 .

Wersja PDF