/Szkoła średnia/Równania/Z kropkami

Zadanie nr 2511034

Rozwiąż równanie 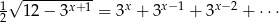1√ ------x+-1 x x−1 x− 2 2 12 − 3 = 3 + 3 + 3 + ⋅⋅ ⋅ .

Wersja PDF

Rozwiązanie

Powinniśmy na początku sprawdzić jaka jest dziedzina równania, ale zamiast to robić, na końcu sprawdzimy otrzymane rozwiązania. Ze wzoru na sumę szeregu geometrycznego mamy

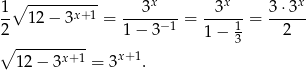
∘ ---------- x x x 1- 12 − 3x+1 = --3-----= -3----= 3⋅-3- 2 1− 3−1 1 − 1 2 ∘ ---------- 3 12 − 3x+ 1 = 3x+ 1.

Oznaczmy 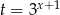t = 3x+ 1 i podnieśmy równanie stronami do kwadratu.

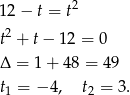
12 − t = t2 2 t + t− 12 = 0 Δ = 1+ 48 = 49 t1 = − 4, t2 = 3.

Pierwsze rozwiązanie odpada i mamy

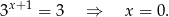
x+1 3 = 3 ⇒ x = 0.

Pozostało sprawdzić, że 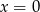x = 0 należy do dziedziny równania. Mamy wtedy iloraz ciągu z prawej strony 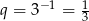q = 3 −1 = 13 i jest OK. Wyrażenie pod pierwiastkiem też jest dodatnie.  
Odpowiedź: x = 0

Wersja PDF