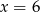/Szkoła średnia/Równania/Z kropkami

Zadanie nr 2664042

Rozwiąż równanie

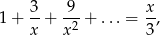
3 9 x 1 + --+ -2-+ ...= -, x x 3

gdzie lewa strona jest sumą kolejnych wyrazów ciągu geometrycznego.

Wersja PDF

Rozwiązanie

Powinniśmy na początku sprawdzić dziedzinę równania, ale zamiast tego sprawdzimy na koniec otrzymane rozwiązania.

Sposób I

Będziemy postępować podobnie, jak przy zwijaniu ułamków okresowych do ułamków zwykłych – przesuniemy wszystkie wyrazy ciągu z lewej strony o jedną pozycję i da nam to pewne równanie na x .

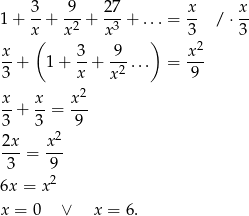
1 + 3-+ 9--+ 27-+ ... = x- / ⋅ x- x( x2 x3 ) 3 3 x- 3- 9-- x-2 3 + 1 + x + x2 ... = 9 x- x- x2- 3 + 3 = 9 2 2x-= x-- 3 9 6x = x2 x = 0 ∨ x = 6.

Rozwiązanie 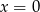x = 0 odpada ze względu na dziedzinę równania, zatem x = 6 .

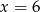Sposób II

Korzystamy ze wzoru na sumę szeregu geometrycznego.

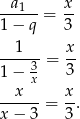
-a1--- x- 1− q = 3 --1---= x- 1− 3 3 x x x ------= --. x− 3 3

Mamy zatem 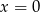x = 0 lub

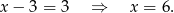
x − 3 = 3 ⇒ x = 6.

Pierwsze rozwiązanie 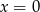x = 0 odrzucamy, bo nie należy do dziedziny równania, a drugie 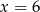x = 6 jest OK, bo wtedy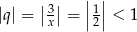 | | | | |q| = |3x| = ||12|| < 1  
Odpowiedź: x = 6

Wersja PDF