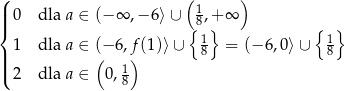/Szkoła średnia/Równania/Z kropkami

Zadanie nr 2701961

Zbadaj liczbę pierwiastków równania 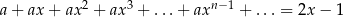2 3 n−1 a+ ax+ ax + ax + ...+ ax + ...= 2x − 1 w zależności od wartości parametru a .

Wersja PDF

Rozwiązanie

Aby lewa strona była zbieżnym szeregiem geometrycznym musi być 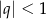|q| < 1 , czyli

|x| < 1 ⇒ x ∈ (− 1,1).

Z wzoru na sumę szeregu geometrycznego mamy

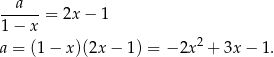
a ------= 2x − 1 1 − x a = (1 − x)(2x − 1) = − 2x2 + 3x − 1.

Ile rozwiązań ma to równanie? – najłatwiej narysować sobie wykres funkcji 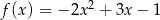2 f (x) = − 2x + 3x − 1 na przedziale 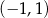(− 1,1 ) i odczytać z wykresu.

PIC

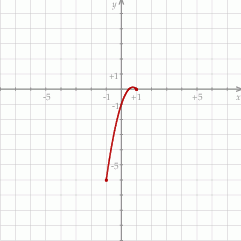
Wierzchołek paraboli będącej wykresem tej funkcji ma współrzedne

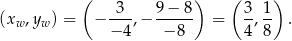
( ) ( ) (xw,yw ) = − -3-,− 9-−-8- = 3, 1 . − 4 − 8 4 8

Łatwo teraz odczytać ilość rozwiązań równania 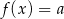f(x) = a .

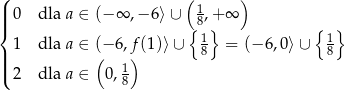
( ( ) ||| 0 dla a ∈ (− ∞ ,− 6⟩∪ 18,+ ∞ { { } { } 1 dla a ∈ (− 6,f(1 )⟩∪ 18 = (− 6,0⟩∪ 18 |||( ( 1) 2 dla a ∈ 0,8

 
Odpowiedź: ( ( ) | 0 dla a ∈ (− ∞ ,−6 ⟩∪ 1,+ ∞ ||{ {8} { } 1 dla a ∈ (− 6,f(1)⟩∪ 1 = (− 6,0⟩ ∪ 1 || ( ) 8 8 |( 2 dla a ∈ 0, 18

Wersja PDF