Zadanie nr 3511588

Rozwiąż równanie

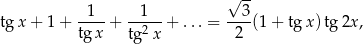
√ -- tgx + 1 + -1--+ -1---+ ...= --3-(1+ tg x) tg 2x, tg x tg 2x 2

w którym lewa strona jest sumą wyrazów nieskończonego ciągu geometrycznego.

Rozwiązanie

Po pierwsze, ze względu na 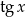tg x , musimy założyć, że

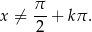
π- x ⁄= 2 + kπ .

Kolejne ograniczenie to iloraz 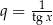q = -1- tg x ciągu geometrycznego musi spełniać warunek

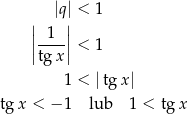
|q| < 1 | | ||--1-|| |tg x| < 1 1 < |tg x| tgx < − 1 lub 1 < tg x

Szkicujemy tangensa.

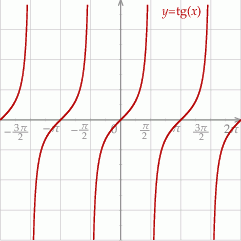
Odczytujemy z wykresu rozwiązanie powyższej nierówności

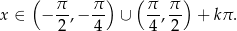
( π π ) ( π π ) x ∈ − --,− -- ∪ --,-- + kπ . 2 4 4 2

Przy powyższych założeniach, dane równanie przybiera postać (korzystamy ze wzoru na sumę szeregu geometrycznego).

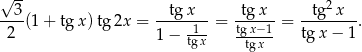
√ -- 2 --3-(1+ tg x) tg 2x = -tg-x---= tg-x--= -tg--x-. 2 1− tg1x tg-x−1- tg x − 1 tg x

Zanim przekształcimy to równanie dalej, zauważmy jeszcze, że

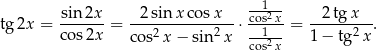
--1-- tg2x = sin-2x-= -2-sin-x-cosx---⋅cos2x = -2-tgx--. cos 2x cos2x − sin2 x co1s2x 1− tg 2x

Wracamy teraz do przekształcania równania.

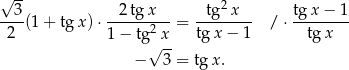
√ -- 3 2 tgx tg2 x tg x− 1 ---(1 + tg x)⋅ ------2--= -------- / ⋅-------- 2 1− tg√ x- tgx − 1 tg x − 3 = tg x.

Rozwiązaniem tego równania jest zbiór

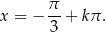
π x = − -- + kπ . 3

Odpowiedź: 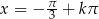π x = − 3-+ kπ , k ∈ Z