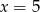Zadanie nr 3917514
Rozwiąż równanie 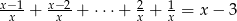 .
.
Rozwiązanie
Skorzystamy ze wzoru na sumę ciągu arytmetycznego:
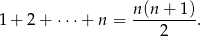
Liczymy
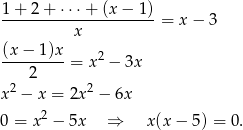
Zatem 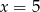 , bo
, bo 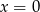 nie należy do dziedziny danego równania.
nie należy do dziedziny danego równania.
Odpowiedź: 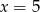
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 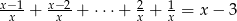 .
.
Skorzystamy ze wzoru na sumę ciągu arytmetycznego:
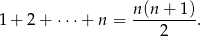
Liczymy
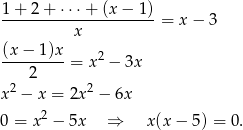
Zatem 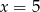 , bo
, bo 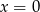 nie należy do dziedziny danego równania.
nie należy do dziedziny danego równania.
Odpowiedź: