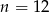Zadanie nr 4039052
Rozwiąż równanie 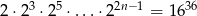 , gdy
, gdy 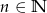 .
.
Rozwiązanie
Przekształćmy lewą stronę równania
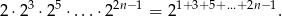
Widać, że wykładnik jest sumą  początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie równym 1 i
początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie równym 1 i  -tym równym
-tym równym 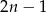 . Zatem
. Zatem
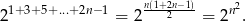
Przekształćmy prawą stronę równania
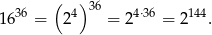
Stąd
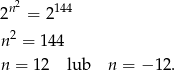
Odrzucamy ujemne rozwiązanie i otrzymujemy, że 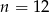 .
.
Odpowiedź: