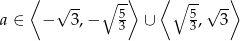Zadanie nr 4089949

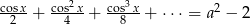Dla jakich wartości parametru równanie cosx- cos2x- cos3x 2 2 + 4 + 8 + ⋅⋅⋅ = a − 2 , ma rozwiązanie?

Rozwiązanie

Lewa strona jest zbieznym szeregiem geometrycznym, o ile

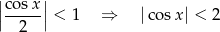
||cosx-|| | 2 | < 1 ⇒ |co sx| < 2

czyli zawsze. Mamy zatem

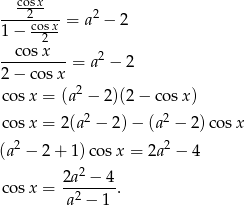
---cos2x--- 2 1 − cosx-= a − 2 2 --co-sx-- = a2 − 2 2 − co sx cosx = (a2 − 2 )(2− cosx) 2 2 cosx = 2(a − 2)− (a − 2 )cosx (a2 − 2 + 1)co sx = 2a2 − 4 2a2 −-4- cosx = a 2 − 1 .

Kiedy to równanie ma rozwiązanie? – lewa strona musi być w przedziale 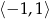⟨− 1,1⟩ .

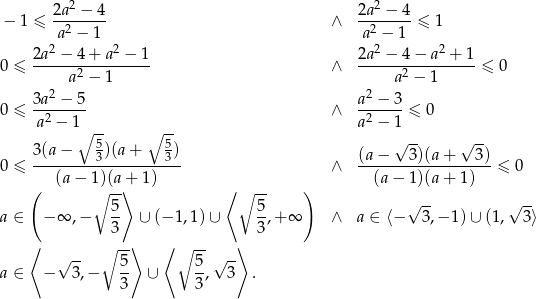
2a 2 − 4 2a2 − 4 − 1 ≤ -------- ∧ --------≤ 1 a2 − 1 a2 − 1 2a2 − 4+ a2 − 1 2a2 − 4 − a2 + 1 0 ≤ -----a2 −-1----- ∧ -----a2-−-1----- ≤ 0 2 2 0 ≤ 3a-−--5- ∧ a--−-3 ≤ 0 a2 − 1 a2 − 1 ∘ 5- ∘ 5- √ -- √ -- 3(a− 3)(a + 3) (a − 3)(a + 3) 0 ≤ ---(a−--1)(a+--1)---- ∧ --(a-−-1)(a-+-1)---≤ 0 ( ∘ --⟩ ⟨ ∘ -- ) 5 5 √ -- √ -- a ∈ − ∞ ,− -- ∪ (− 1,1) ∪ --,+ ∞ ∧ a ∈ ⟨− 3,− 1)∪ (1 , 3⟩ ⟨ 3 ⟩ ⟨ ⟩ 3 √ -- ∘ -5 ∘ 5-√ -- a ∈ − 3,− -- ∪ -, 3 . 3 3

Odpowiedź: ⟨ √ -- ∘ -⟩ ⟨ ∘ --√ -⟩ a ∈ − 3,− 5 ∪ 5, 3 3 3