Zadanie nr 4270953

Znajdź największą liczbę naturalną 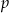, dla której ciąg 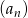(an) , określony wzorem 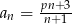an = pnn++31- jest malejący. Dla znalezionej wartości 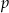rozwiąż równanie

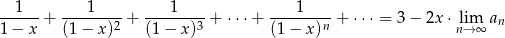
--1--- ---1----- ----1---- ----1---- 1− x + (1 − x)2 + (1 − x )3 + ⋅ ⋅⋅+ (1 − x )n + ⋅⋅⋅ = 3− 2x ⋅ lni→m∞an

Rozwiązanie

Ciąg jest malejący jeżeli 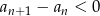an+1 − an < 0 . Sprawdźmy kiedy tak jest.

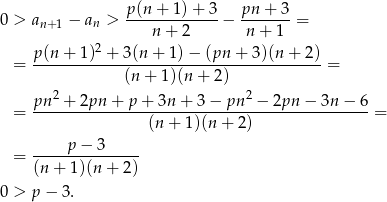
p(n + 1) + 3 pn + 3 0 > an+1 − an > -------------− ------- = n + 2 n + 1 p(n-+-1-)2 +-3(n-+-1)−-(pn--+-3)(n-+-2)- = (n + 1 )(n+ 2) = pn-2 +-2pn-+-p-+-3n-+-3-−-pn-2 −-2pn-−-3n-−--6 = (n+ 1)(n + 2) = = -----p−--3----- (n + 1)(n + 2) 0 > p − 3.

Zatem maksymalna wartość naturalna to 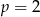p = 2 . Policzmy granicę tego ciągu.

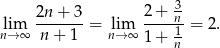
3 lim 2n-+-3-= lim 2+--n-= 2. n→ ∞ n + 1 n→∞ 1+ 1n

Pozostało rozwiązać równanie

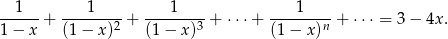
---1-- ---1----- ----1---- ----1---- 1 − x + (1 − x)2 + (1 − x)3 + ⋅ ⋅⋅+ (1 − x )n + ⋅⋅⋅ = 3− 4x.

Sprawdźmy najpierw jaka jest dziedzina tego równania (szereg z lewej strony musi być zbieżny)

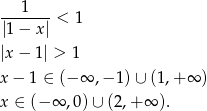
---1---< 1 |1− x| |x − 1 | > 1 x− 1 ∈ (− ∞ ,− 1)∪ (1,+ ∞ ) x ∈ (− ∞ ,0)∪ (2 ,+ ∞ ).

Teraz pora na równanie

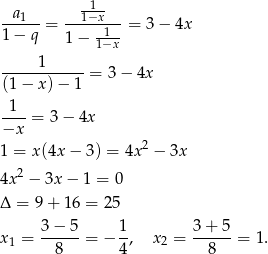
-1-- -a1---= --1−x---= 3− 4x 1− q 1− 11−x- 1 ------------= 3 − 4x (1− x)− 1 1 ----= 3 − 4x −x 2 1 = x(4x − 3 ) = 4x − 3x 4x2 − 3x − 1 = 0 Δ = 9 + 1 6 = 25 3 − 5 1 3 + 5 x1 = ------= − -, x 2 = ------= 1. 8 4 8

Tylko pierwsze z rozwiązań należy do dziedziny równania.
Odpowiedź: 1 x = − 4