/Szkoła średnia/Równania/Z kropkami

Zadanie nr 4471274

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 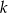k równanie 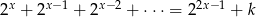x x− 1 x−2 2x−1 2 + 2 + 2 + ⋅⋅⋅ = 2 + k ma dokładnie jedno rozwiązanie?

Rozwiązanie

Lewa strona jest zbieżnym szeregiem geometrycznym (o ilorazie 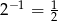− 1 1 2 = 2 ), możemy więc zastosować wzór na sumę szeregu geometrycznego.

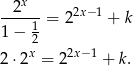
x --2---= 22x−1 + k 1 − 12 x 2x−1 2 ⋅2 = 2 + k.

Jeżeli podstawimy 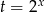x t = 2 to mamy

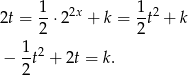
1 1 2t = --⋅2 2x + k = -t2 + k 2 2 1-2 − 2 t + 2t = k.

Kiedy to równanie ma dokładnie jedno rozwiązanie? – najłatwiej narysować wykres funkcji 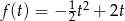f(t) = − 1t2 + 2t 2 na przedziale 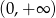(0,+ ∞ ) (takie wartości przyjmuje t = 2x ).

PIC

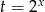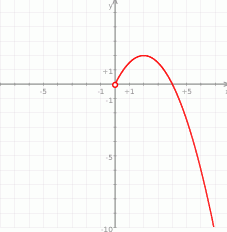
Wierzchołek tej paraboli jest w punkcie 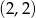(2,2) i z wykresu widać, że jedno rozwiązanie będzie dla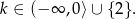 k ∈ (− ∞ ,0⟩ ∪ {2}.  
Odpowiedź: k ∈ (− ∞ ,0⟩ ∪ {2}

Wersja PDF