Zadanie nr 5485125
O funkcji 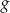 wiadomo, że
wiadomo, że 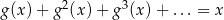 , gdzie lewa strona równania jest sumą szeregu geometrycznego zbieżnego. Dla jakich wartości parametru
, gdzie lewa strona równania jest sumą szeregu geometrycznego zbieżnego. Dla jakich wartości parametru 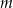 równanie
równanie 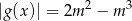 posiada dwa rozwiązania?
posiada dwa rozwiązania?
Rozwiązanie
Sprawdźmy najpierw jaki wzór musi mieć funkcja 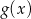 , tak żeby
, tak żeby
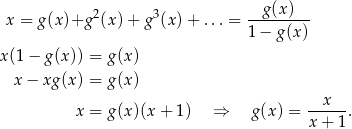
Powyższy rachunek ma sens o ile
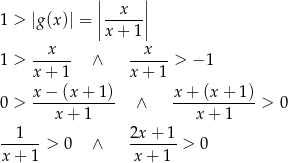
Lewa nierówność oznacza, że 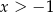 , więc z prawej nierówności mamy
, więc z prawej nierówności mamy
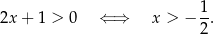
Dziedziną funkcji 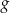 jest więc przedział
jest więc przedział 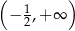 .
.
Szkicujemy teraz wykres funkcji
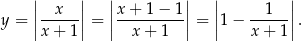
Funkcja pod wartością bezwzględną to hiperbola 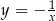 przesunięta o wektor
przesunięta o wektor ![[− 1,1]](https://img.zadania.info/zad/5485125/HzadR9x.gif) . Potem musimy jeszcze odbić część poniżej osi
. Potem musimy jeszcze odbić część poniżej osi 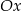 do góry.
do góry.
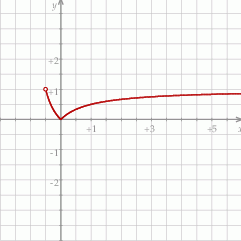
Z wykresu widać, że dane równanie będzie miało dwa rozwiązania wtedy i tylko wtedy, gdy
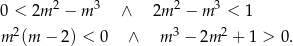
Lewa nierówność jest spełniona dla 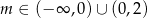 . Zanim rozwiążemy prawą nierówność, rozłóżmy znajdujący się w niej wielomian. Widać, że jednym z jego pierwiastków jest
. Zanim rozwiążemy prawą nierówność, rozłóżmy znajdujący się w niej wielomian. Widać, że jednym z jego pierwiastków jest 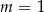 , więc dzielimy go przez
, więc dzielimy go przez 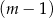 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
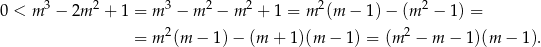
Rozkładamy jeszcze trójmian w pierwszym nawiasie.
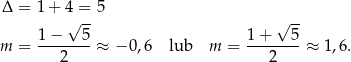
Mamy więc nierówność
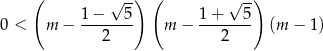
i jej rozwiązaniem jest zbiór
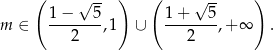
Łączymy ten warunek z otrzymanym wcześniej warunkiem 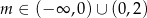 mamy
mamy
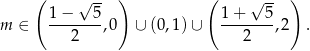
Odpowiedź: