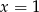Zadanie nr 7251930
Rozwiąż równanie 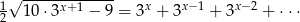 .
.
Rozwiązanie
Na początku powinniśmy sprawdzić dziedzinę równania, ale zamiast tego sprawdzimy na koniec otrzymane rozwiązania.
Prawa strona równania jest sumą szeregu geometrycznego o ilorazie 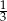 . Zatem możemy podane równanie zapisać w postaci
. Zatem możemy podane równanie zapisać w postaci
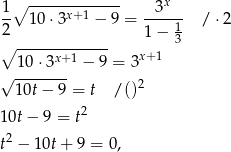
gdzie podstawiliśmy 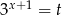 . Dalej mamy
. Dalej mamy 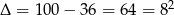 ,
, 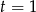 lub
lub 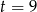 . Stąd
. Stąd 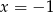 lub
lub 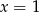 .
.
Łatwo sprawdzić, że oba rozwiązania należą do dziedziny równania (otrzymane liczby pod pierwiastkiem są dodatnie).
Odpowiedź: 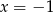 lub
lub