/Szkoła średnia/Równania/Z kropkami

Zadanie nr 7483432

Dana jest funkcja

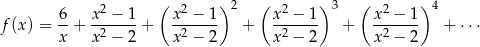
2 ( 2 ) 2 ( 2 )3 ( 2 )4 f(x) = 6-+ x--−-1-+ x-−--1- + x--−-1- + x--−-1- + ⋅⋅⋅ x x 2 − 2 x2 − 2 x 2 − 2 x2 − 2

Wyznacz dziedzinę i miejsca zerowe funkcji 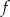f .

Wersja PDF

Rozwiązanie

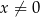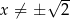Ze względu na miejsca zerowe mianowników musi być x ⁄= 0 i √ -- x ⁄= ± 2 . Ponadto, musimy mieć pewność, że szereg geometryczny definiujący funkcję 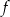f jest zbieżny, czyli

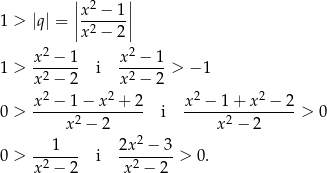
| | ||x2 −-1|| 1 > |q| = |x2 − 2| 2 2 1 > x--−-1- i x--−-1-> − 1 x2 − 2 x2 − 2 x2 − 1 − x2 + 2 x2 − 1+ x2 − 2 0 > ------2--------- i ------2---------> 0 x − 2 x − 2 ---1--- 2x2-−-3- 0 > x2 − 2 i x 2 − 2 > 0.

Rozwiązaniem pierwszej nierówności jest przedział

√ --√ -- (− 2, 2).

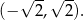
Ponadto, przy tym założeniu 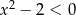2 x − 2 < 0 , więc druga nierówność jest równoważna nierówności

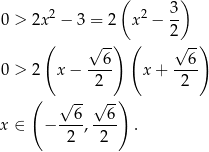
( 3) 0 > 2x2 − 3 = 2 x2 − -- ( ) ( 2 ) √ 6- √ 6- 0 > 2 x − ---- x + ---- 2 2 ( √ --√ --) x ∈ − --6,--6- . 2 2

Ponieważ 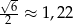√6- 2 ≈ 1,2 2 , łącząc wszystkie otrzymane warunki otrzymujemy

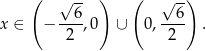
( √ -- ) ( √ -) x ∈ − --6,0 ∪ 0,--6- . 2 2

Przy tym założeniu szereg definiujący funkcję 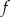f jest zbieżny i mamy

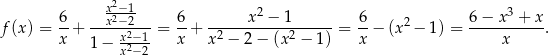
x2−1 2 3 f(x) = 6-+ --x2−2---= 6-+ ------x-−--1------= 6-− (x2 − 1) = 6-−-x--+-x-. x 1 − x22−1 x x 2 − 2 − (x2 − 1) x x x −2

Szukamy teraz miejsc zerowych wielomianu

x3 − x− 6.

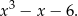
Sprawdzamy najpierw dzielniki wyrazu wolnego – gdy to zrobimy znajdziemy pierwiastek 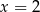x = 2 . Dzielimy teraz ten wielomian przez 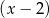(x − 2) – my zrobimy to grupując wyrazy.

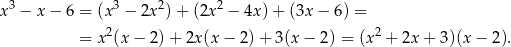
x3 − x− 6 = (x3 − 2x 2) + (2x 2 − 4x )+ (3x− 6) = 2 2 = x (x − 2 )+ 2x (x− 2)+ 3(x− 2) = (x + 2x + 3)(x − 2).

Trójmian w nawiasie ma ujemną 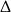Δ -ę, więc jedynym pierwiastkiem jest 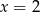x = 2 . Jednak liczba ta nie należy do dziedziny funkcji, więc funkcja 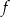f nie posiada miejsc zerowych.  
Odpowiedź: 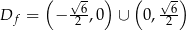( √- ) ( √ -) Df = − -6,0 ∪ 0,--6 2 2 . Brak miejsc zerowych.

Wersja PDF