/Szkoła średnia/Równania/Z kropkami

Zadanie nr 8425480

Rozwiąż równanie:

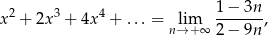
1 − 3n x2 + 2x3 + 4x4 + ...= lim -------, n→ +∞ 2 − 9n

gdzie lewa strona równania jest sumą nieskończonego ciągu geometrycznego.

Wersja PDF

Rozwiązanie

Obliczamy najpierw granicę z prawej strony równania (dzielimy licznik i mianownik przez n )

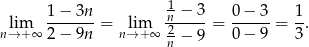
1 lim 1-−-3n-= lim -n −-3 = 0-−-3-= 1-. n→ +∞ 2 − 9n n→ +∞ 2− 9 0 − 9 3 n

Sprawdźmy teraz, kiedy szereg z lewej strony równania jest zbieżny. Jego iloraz jest równy

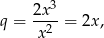
2x 3 q = ---- = 2x , x2

więc mamy nierówność

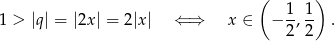
( 1 1) 1 > |q| = |2x| = 2|x| ⇐ ⇒ x ∈ − --,-- . 2 2

Przy tym założeniu równanie możemy zapisać postaci

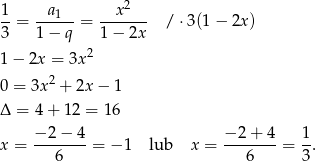
1 a x2 --= ---1--= ------- / ⋅3(1 − 2x) 3 1 − q 1 − 2x 1 − 2x = 3x2 0 = 3x2 + 2x − 1 Δ = 4 + 12 = 16 −-2-−-4 −-2-+-4 1- x = 6 = − 1 lub x = 6 = 3.

Tylko druga z tych liczb jest w przedziale 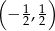( ) − 12, 12 , więc równanie ma jedno rozwiązanie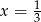 1 x = 3  
Odpowiedź: x = 13

Wersja PDF