Zadanie nr 8875612
Rozwiąż równanie 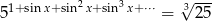 .
.
Rozwiązanie
Jeżeli zapiszemy równanie w postaci
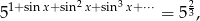
to widać, że musimy rozwiązać równanie
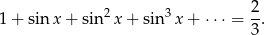
Lewa strona jest zbieżnym szeregiem geometrycznym, o ile 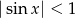 , czyli
, czyli 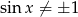 . Mamy wtedy
. Mamy wtedy
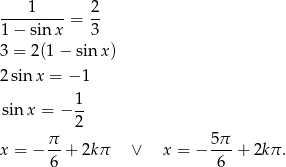
Odpowiedź: 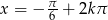 lub
lub 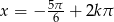 dla
dla 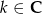 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 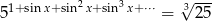 .
.
Jeżeli zapiszemy równanie w postaci
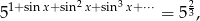
to widać, że musimy rozwiązać równanie
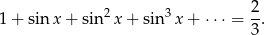
Lewa strona jest zbieżnym szeregiem geometrycznym, o ile 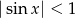 , czyli
, czyli 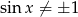 . Mamy wtedy
. Mamy wtedy
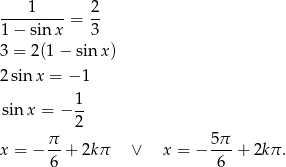
Odpowiedź: 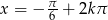 lub
lub 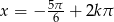 dla
dla 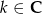 .
.
