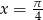Dany jest nieskończony ciąg geometryczny frac{1}{sin x+cos ... Zadania.info: rozwiązanie zadania, Z kropkami, 8952681

Forum

Równania

Zadanie nr 8952681

Dany jest nieskończony ciąg geometryczny

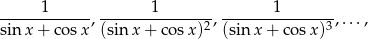
1 1 1 ------------, --------------2,--------------3-,..., sinx + co sx (sin x + cos x) (sin x+ cosx)

gdzie 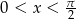$π 0 < x < 2-$ .

Wykaż, że dany ciąg jest malejący.
Wyznacz sumę 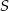$S$ wszystkich wyrazów tego ciągu.
Wiedząc, że suma 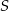$S$ wszystkich wyrazów tego ciągu wynosi 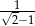$√-1-- 2− 1$ , oblicz $x$ .

Rozwiązanie

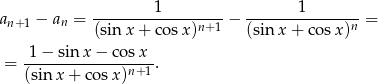
Policzmy różnicę dwóch sąsiednich wyrazów. $a − a = --------1---------− -------1-------- = n+1 n (sin x + cos x)n+1 (sin x+ cosx )n 1− sin x − cos x = ------------------. (sinx + co sx)n+ 1$
Wystarczy pokazać, że
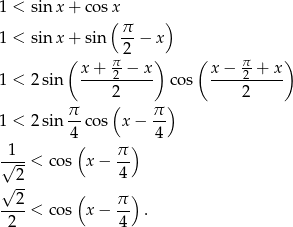
$1 < sin x + cos(x ) 1 < sin x + sin π-− x 2 ( x + π-− x) ( x − π-+ x) 1 < 2sin -----2---- cos -----2---- 2( ) 2 1 < 2sin π-cos x − π- 4 4 1 ( π ) √---< cos x − -4 √ 2- --2- ( π-) 2 < cos x − 4 .$
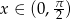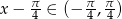Jeżeli $π- x ∈ (0,2 )$ , to $π- π- π- x− 4 ∈ (− 4,4 )$ i powyższa nierówność jest spełniona.
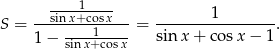
Liczymy $----1---- S = --sinx+cosx-- = -------1--------. 1 − sinx1+cosx sin x + cos x− 1$

Odpowiedź: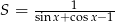 $S = sinx+1cosx−1$
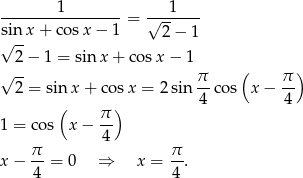
Musimy rozwiązać równanie $1 1 -----------------= √------- s√inx + co sx − 1 2− 1 2− 1 = sinx + co sx − 1 √ -- π ( π ) 2 = sinx + co sx = 2 sin --cos x − -- ( ) 4 4 1 = cos x − π- 4 x− π-= 0 ⇒ x = π-. 4 4$

Odpowiedź: $π- x = 4$

Twoje uwagi

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!