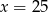/Szkoła średnia/Równania/Z kropkami

Zadanie nr 9520388

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 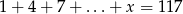1+ 4+ 7+ ...+ x = 1 17 , w którym lewa strona jest sumą kolejnych wyrazów ciągu arytmetycznego.

Rozwiązanie

Lewa strona podanego równania jest sumą wyrazów ciągu arytmetycznego o pierwszym wyrazie 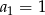a1 = 1 i różnicy 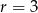r = 3 . Korzystając ze wzoru na sumę wyrazów ciągu arytmetycznego, mamy

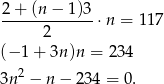
2-+-(n-−-1)3- 2 ⋅n = 117 (− 1+ 3n)n = 234 3n2 − n − 234 = 0.

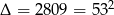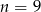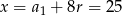Dalej, Δ = 2809 = 532 . Dodatni pierwiastek to n = 9 . Zatem x = a1 + 8r = 2 5 .  
Odpowiedź: x = 25

Wersja PDF