Zadanie nr 9402236
Halina narysowała kwadrat o wymiarach 5x5 i zaznaczyła na rysunku środki kwadracików jednostkowych. Następnie umieściła przeszkody (pogrubione linie – patrz rysunek) i badała, na ile sposobów można przejść od punktu 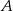 do punktu
do punktu 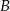 najkrótszą drogą, idąc pionowymi lub poziomymi odcinkami od środka kwadracika do środka kwadracika i omijając przeszkody. Ile jest takich najkrótszych dróg?
najkrótszą drogą, idąc pionowymi lub poziomymi odcinkami od środka kwadracika do środka kwadracika i omijając przeszkody. Ile jest takich najkrótszych dróg?

A) 6 B) 8 C) 9 D) 11 E) 12
Rozwiązanie
Poruszamy się od kwadratu 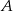 do
do 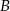 wpisując w każdym z kwadratów liczbę prowadzących do niego dróg. Liczba ta to suma liczb z wszystkich poprzedzających wierzchołków (rysunek). Gdy wypełnimy wszystkie pola, okaże się, że jest 12 dróg.
wpisując w każdym z kwadratów liczbę prowadzących do niego dróg. Liczba ta to suma liczb z wszystkich poprzedzających wierzchołków (rysunek). Gdy wypełnimy wszystkie pola, okaże się, że jest 12 dróg.

Odpowiedź: E

