Zadanie nr 1459498
Podstawą ostrosłupa 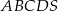 jest kwadrat
jest kwadrat 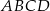 . Krawędź boczna
. Krawędź boczna 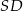 jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi
jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi 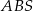 i
i 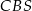 tego ostrosłupa.
tego ostrosłupa.
Rozwiązanie
Szkicujemy ostrosłup.
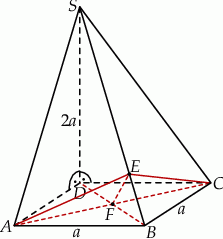
Zauważmy, że krawędź 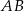 jest prostopadła do
jest prostopadła do 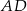 i do
i do 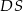 (bo jest równoległa do
(bo jest równoległa do 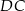 ). To oznacza, że krawędź
). To oznacza, że krawędź 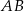 jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 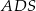 . Jest więc prostopadła do każdej prostej zawartej w tej płaszczyźnie, w szczególności trójkąt
. Jest więc prostopadła do każdej prostej zawartej w tej płaszczyźnie, w szczególności trójkąt 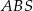 jest prostokątny.
jest prostokątny.
Analogicznie wykazujemy, że trójkąt 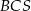 jest prostokątny. Obliczamy teraz długości krawędzi
jest prostokątny. Obliczamy teraz długości krawędzi 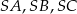 ostrosłupa.
ostrosłupa.
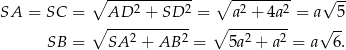
Aby zaznaczyć kąt między ścianami 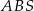 i
i 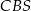 ostrosłupa dorysowujemy wysokości
ostrosłupa dorysowujemy wysokości 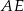 i
i 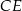 ścian bocznych (płaszczyzna
ścian bocznych (płaszczyzna 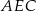 jest prostopadła do krawędzi wspólnej
jest prostopadła do krawędzi wspólnej 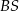 ścian
ścian 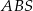 i
i 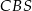 , więc kąt
, więc kąt 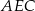 jest interesującym nas kątem między tymi ścianami).
jest interesującym nas kątem między tymi ścianami).
Wysokość 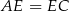 trójkąta prostokątnego
trójkąta prostokątnego 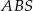 możemy obliczyć porównując dwa wzory na pole.
możemy obliczyć porównując dwa wzory na pole.
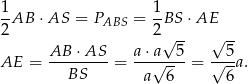
Sinus kąta 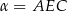 obliczymy na dwa sposoby.
obliczymy na dwa sposoby.
Sposób I
Odcinek 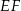 jest wysokością w trójkącie równoramiennym
jest wysokością w trójkącie równoramiennym 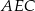 , więc
, więc
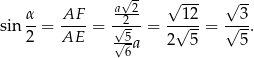
Obliczamy teraz 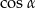 .
.
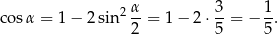
Pozostało obliczyć teraz 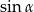 .
.
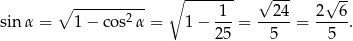
Sposób II
Tym razem obliczamy 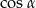 pisząc twierdzenie cosinusów w trójkącie
pisząc twierdzenie cosinusów w trójkącie 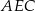 .
.
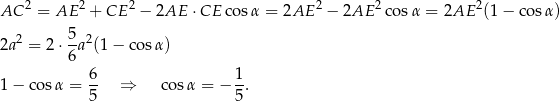
Pozostało obliczyć teraz 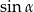 .
.
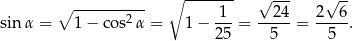
Odpowiedź: