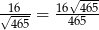Zadanie nr 2386073
Podstawą ostrosłupa 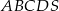 jest kwadrat
jest kwadrat 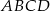 . Trójkąt równoramienny
. Trójkąt równoramienny 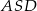 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 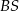 ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny
ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny 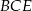 do płaszczyzny podstawy, gdzie
do płaszczyzny podstawy, gdzie 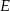 jest środkiem krawędzi
jest środkiem krawędzi 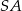 .
.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
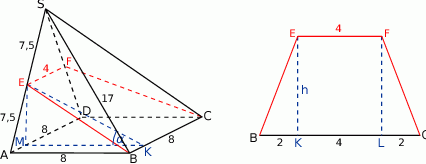
Przekrój ostrosłupa płaszczyzną 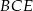 jest trapezem równoramiennym
jest trapezem równoramiennym 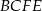 , gdzie
, gdzie 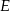 i
i 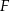 środki krawędzi
środki krawędzi 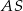 i
i 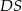 . Kąt
. Kąt  między płaszczyzną
między płaszczyzną 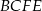 , a płaszczyzną podstawy otrzymamy przecinając te płaszczyzny płaszczyzną prostopadłą do ich wspólnej krawędzi
, a płaszczyzną podstawy otrzymamy przecinając te płaszczyzny płaszczyzną prostopadłą do ich wspólnej krawędzi 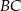 . Jeżeli poprowadzimy ten przekrój przez punkt
. Jeżeli poprowadzimy ten przekrój przez punkt 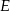 , to otrzymamy trójkąt
, to otrzymamy trójkąt 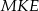 , gdzie
, gdzie 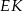 to wysokość trapezu
to wysokość trapezu 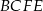 , a
, a 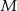 rzut punktu
rzut punktu 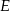 na płaszczyznę podstawy. Musimy zatem obliczyć długości odcinków
na płaszczyznę podstawy. Musimy zatem obliczyć długości odcinków 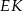 i
i 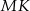 .
.
Zauważmy, że trójkąt 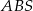 jest prostokątny (bo prosta
jest prostokątny (bo prosta 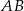 jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 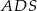 ). To pozwala obliczyć długość krawędzi kwadratu w podstawie.
). To pozwala obliczyć długość krawędzi kwadratu w podstawie.
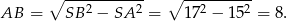
Długość odcinka 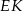 obliczymy na dwa sposoby.
obliczymy na dwa sposoby.
Sposób I
Wiemy jakie są długości podstaw trapezu 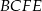 :
: 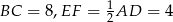 . Potrzebujemy jeszcze jego wysokości. Obliczmy najpierw długość odcinka
. Potrzebujemy jeszcze jego wysokości. Obliczmy najpierw długość odcinka 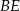 . Pamiętamy, że
. Pamiętamy, że 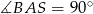 , zatem
, zatem
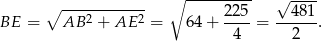
Rysujemy teraz z boku trapez 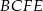 i zaznaczamy jego wysokości
i zaznaczamy jego wysokości 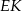 i
i 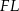 . Z trójkąta prostokątnego
. Z trójkąta prostokątnego 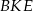 mamy
mamy
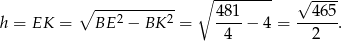
Pozostało obliczyć 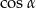 .
.
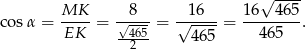
Sposób II
Obliczmy najpierw długość odcinka 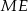 . Jest on równy połowie wysokości trójkąta
. Jest on równy połowie wysokości trójkąta 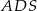 , czyli ma długość
, czyli ma długość
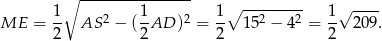
Z trójkąta prostokątnego 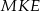 obliczamy długość odcinka
obliczamy długość odcinka 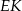 .
.
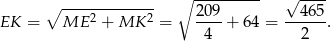
Cosinus kąta  obliczamy jak poprzednio.
obliczamy jak poprzednio.
Odpowiedź: