/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny/Kwadrat w podstawie

Zadanie nr 3570758

Podstawą ostrosłupa prawidłowego czworokątnego 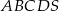ABCDS jest kwadrat 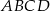ABCD . Pole trójkąta równoramiennego 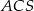ACS jest równe 120 oraz 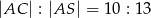|AC | : |AS | = 10 : 13 . Oblicz pole powierzchni bocznej tego ostrosłupa.

Wersja PDF

Rozwiązanie

Oznaczmy krawędź podstawy ostrosłupa przez a .

PIC

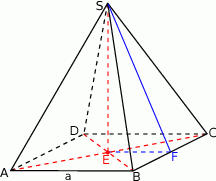
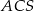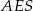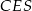Trójkąt ACS składa się z dwóch przystających trójkątów prostokątnych AES i CES , więc pole każdego z nich jest równe 60. Ponadto wiemy, że

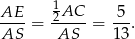
AE 1AC 5 ----= 2----= ---. AS AS 13

Ponadto 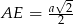√ - AE = a-2- 2 (przekątna w kwadracie). Możemy więc wyliczyć pozostałe boki trójkąta AES .

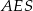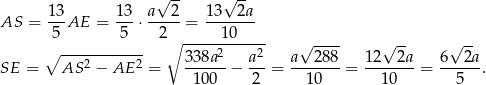
√ -- √ -- AS = 13-AE = 13-⋅ a-2-= 13--2a- 5 5 2∘ -----10----- √ ---- √ -- √ -- ∘ ------------ 338a 2 a2 a 288 12 2a 6 2a SE = AS 2 − AE 2 = ------− ---= ------- = -------= ------. 100 2 10 10 5

Korzystamy teraz ze znanego pola trójkąta 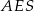AES .

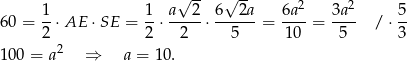
√ -- √ -- 2 2 60 = 1-⋅AE ⋅SE = 1-⋅ a-2-⋅ 6--2a-= 6a--= 3a-- / ⋅ 5 2 2 2 5 10 5 3 100 = a2 ⇒ a = 10 .

Aby wyliczyć pole ściany bocznej potrzebujemy długość jej wysokości 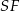SF . Wyliczamy ją z trójkąta prostokątnego EFS .

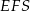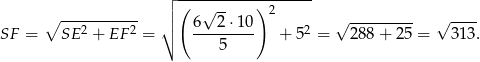
┌│ (--√------)-2------ ∘ ----------- │∘ 6 2⋅ 10 √ --------- √ ---- SF = SE 2 + EF 2 = --------- + 52 = 288 + 25 = 313. 5

Zatem pole ściany bocznej jest równe

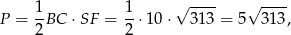
1 1 √ ---- √ ---- P = 2BC ⋅SF = 2-⋅10 ⋅ 313 = 5 313,

a całe pole boczne jest 4 razy większe.  
Odpowiedź: √ ---- 20 3 13

Wersja PDF