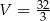/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny/Kwadrat w podstawie

Zadanie nr 5770263

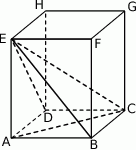
W graniastosłupie prawidłowym czworokątnym 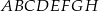ABCDEF GH przekątna 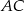AC podstawy ma długość 4. Kąt 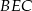BEC jest równy 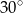30∘ . Oblicz objętość ostrosłupa ABCDE przedstawionego na poniższym rysunku.

PIC

Wersja PDF

Rozwiązanie

Obliczmy najpierw długość krawędzi podstawy. Korzystając ze wzoru na długość przekątnej kwadratu mamy

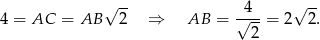
√ -- √ -- 4 = AC = AB 2 ⇒ AB = √4--= 2 2. 2

Trójkąt 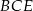BCE jest prostokątny i znamy miarę jego kąta ostrego 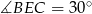∡BEC = 3 0∘ . Mamy zatem

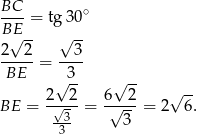
BC-- ∘ BE = tg 30 2√ 2- √ 3- -----= ---- BE √ 3- √ -- 2 2 6 2 √ -- BE = -√3--= √----= 2 6. -3- 3

Liczymy teraz wysokość ostrosłupa. Patrzymy na trójkąt prostokątny 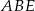ABE .

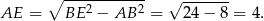
∘ ------------ √ ------- AE = BE 2 − AB 2 = 24 − 8 = 4.

Liczymy objętość ostrosłupa

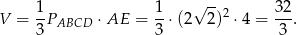
1- 1- √ --2 32- V = 3PABCD ⋅AE = 3 ⋅(2 2) ⋅4 = 3 .

 
Odpowiedź: 32 V = 3

Wersja PDF