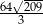/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny/Kwadrat w podstawie

Zadanie nr 8369842

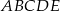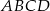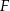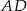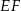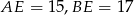Podstawą ostrosłupa ABCDE jest kwadrat ABCD . Punkt F jest środkiem krawędzi AD , odcinek EF jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że AE = 15,BE = 17 .

PIC

Wersja PDF

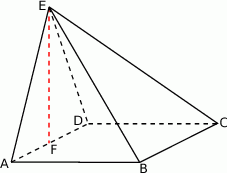
Rozwiązanie

Skoro odcinek 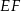EF jest wysokością ostrosłupa, to płaszczyzna 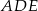ADE musi być prostopadła do podstawy ABCD .

PIC

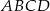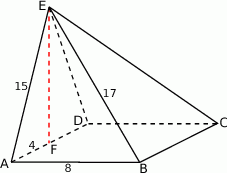
W szczególności trójkąt 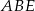ABE jest prostokątny i z twierdzenia Pitagorasa możemy wyliczyć długość krawędzi podstawy.

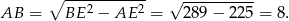
∘ ----------- √ ---------- AB = BE 2 − AE 2 = 28 9− 2 25 = 8.

Wysokość 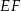EF ostrosłupa wyliczamy z trójkąta prostokątnego AF E .

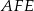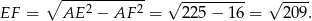
∘ ------------ √ --------- √ ---- EF = AE 2 − AF 2 = 225− 16 = 20 9.

Zatem objętość jest równa

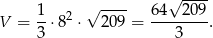
√ ---- 1- 2 √ ---- 64--2-09 V = 3 ⋅8 ⋅ 20 9 = 3 .

 
Odpowiedź: √ --- 64--209 3

Wersja PDF