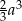Zadanie nr 8636937
Podstawą ostrosłupa 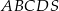 jest kwadrat
jest kwadrat 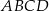 o boku długości
o boku długości  , a krawędź boczna
, a krawędź boczna 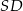 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi 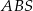 i
i 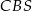 tego ostrosłupa jest równy
tego ostrosłupa jest równy 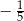 .
.
Rozwiązanie
Szkicujemy ostrosłup.
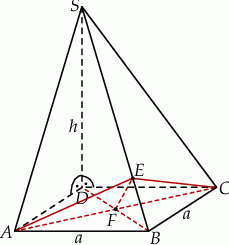
Zauważmy, że krawędź 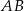 jest prostopadła do
jest prostopadła do 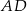 i do
i do 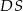 (bo jest równoległa do
(bo jest równoległa do 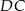 ). To oznacza, że krawędź
). To oznacza, że krawędź 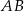 jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 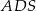 . Jest więc prostopadła do każdej prostej zawartej w tej płaszczyźnie, w szczególności trójkąt
. Jest więc prostopadła do każdej prostej zawartej w tej płaszczyźnie, w szczególności trójkąt 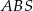 jest prostokątny. Analogicznie wykazujemy, że trójkąt
jest prostokątny. Analogicznie wykazujemy, że trójkąt 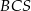 jest prostokątny.
jest prostokątny.
Aby zaznaczyć kąt między ścianami 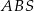 i
i 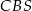 ostrosłupa dorysowujemy wysokości
ostrosłupa dorysowujemy wysokości 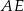 i
i 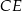 ścian bocznych (płaszczyzna
ścian bocznych (płaszczyzna 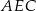 jest prostopadła do krawędzi wspólnej
jest prostopadła do krawędzi wspólnej 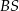 ścian
ścian 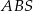 i
i 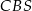 , więc kąt
, więc kąt 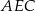 jest interesującym nas kątem między tymi ścianami).
jest interesującym nas kątem między tymi ścianami).
Obliczymy teraz długość wysokości 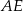 trójkąta
trójkąta 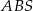 . W tym celu piszemy twierdzenie cosinusów w trójkącie równoramiennym
. W tym celu piszemy twierdzenie cosinusów w trójkącie równoramiennym 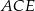 .
.
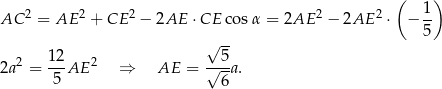
Oznaczmy teraz przez 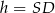 wysokość ostrosłupa. Jak wcześniej zauważyliśmy trójkąt
wysokość ostrosłupa. Jak wcześniej zauważyliśmy trójkąt 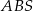 jest prostokątny. Obliczmy długości jego boków
jest prostokątny. Obliczmy długości jego boków 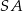 i
i 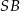 .
.
Porównujemy teraz dwa wzory na pole trójkąta  (inny sposób to skorzystanie z podobieństwa trójkątów
(inny sposób to skorzystanie z podobieństwa trójkątów  i
i 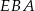 ).
).
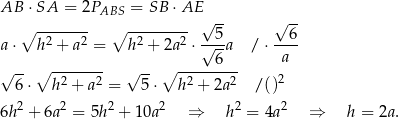
Pozostało obliczyć objętość ostrosłupa
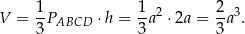
Odpowiedź: