Zadanie nr 9483487
Podstawą ostrosłupa 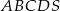 jest kwadrat
jest kwadrat 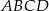 o boku długości 4. Odcinek
o boku długości 4. Odcinek 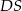 jest wysokością ostrosłupa i ma długość 6. Punkt
jest wysokością ostrosłupa i ma długość 6. Punkt 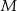 jest środkiem odcinka
jest środkiem odcinka 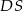 . Oblicz pole przekroju ostrosłupa płaszczyzną
. Oblicz pole przekroju ostrosłupa płaszczyzną 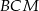 .
.
Rozwiązanie
Typowe zadanie na wyobraźnię. Wyobraźni trzeba umieć pomóc, więc ważny jest tu odpowiedni rysunek. Mi osobiście wygodnie jest myśleć o tym ostrosłupie jako o leżącym na jednej z bocznych ścian.
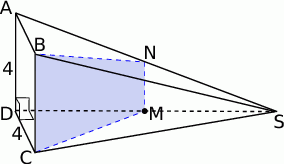
Wiemy, że krawędź 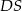 jest prostopadła do podstawy, zatem prostopadłe do podstawy są też ściany
jest prostopadła do podstawy, zatem prostopadłe do podstawy są też ściany 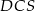 i
i 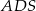 . Ponieważ prosta
. Ponieważ prosta 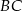 jest równoległa do ściany
jest równoległa do ściany 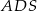 (bo jest równoległa do
(bo jest równoległa do 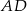 ), więc odcinki
), więc odcinki 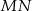 i
i 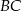 są równoległe. Ponadto, ponieważ
są równoległe. Ponadto, ponieważ 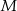 jest środkiem
jest środkiem 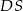 , mamy
, mamy 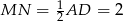 . Aby obliczyć pole trapezu
. Aby obliczyć pole trapezu 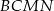 musimy jeszcze wyliczyć jego wysokość. Zauważmy jednak, że prosta
musimy jeszcze wyliczyć jego wysokość. Zauważmy jednak, że prosta 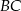 jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 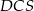 (bo jest równoległa do
(bo jest równoległa do 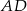 , a
, a 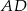 ma tę własność). Zatem trapez
ma tę własność). Zatem trapez 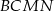 jest prostokątny, czyli jego wysokość to długość odcinka
jest prostokątny, czyli jego wysokość to długość odcinka 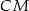 . Długość tego odcinka możemy wyliczyć z trójkąta prostokątnego
. Długość tego odcinka możemy wyliczyć z trójkąta prostokątnego 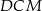
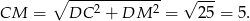
Mamy więc już wszystko co potrzeba do wyliczenia pola trapezu.
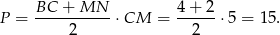
Uwaga. Wiele osób pyta się dlaczego w treści zadania jest mowa o płaszczyźnie 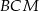 pomimo, że interesujący nas przekrój jest trapezem. Powód jest prosty: płaszczyzna jest wyznaczona przez 3, a nie przez 4 punkty. Przekrój płaszczyzną
pomimo, że interesujący nas przekrój jest trapezem. Powód jest prosty: płaszczyzna jest wyznaczona przez 3, a nie przez 4 punkty. Przekrój płaszczyzną 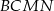 jest tak samo dziwnym sformułowaniem jak prosta
jest tak samo dziwnym sformułowaniem jak prosta 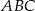 .
.
Odpowiedź: 15

