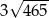/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny/Kwadrat w podstawie

Zadanie nr 9876068

Podstawą ostrosłupa 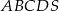ABCDS jest kwadrat 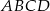ABCD . Trójkąt równoramienny 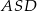ASD ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 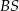BS ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną 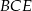BCE , gdzie 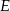E jest środkiem krawędzi SA .

Wersja PDF

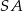Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

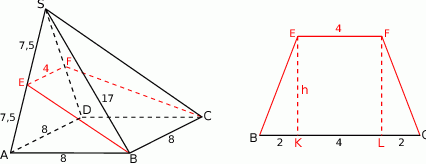
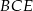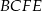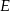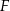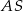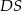Przekrój ostrosłupa płaszczyzną BCE jest trapezem równoramiennym BCF E , gdzie E i F środki krawędzi AS i DS . Zauważmy ponadto, że trójkąt 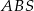ABS jest prostokątny (bo prosta 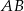AB jest prostopadła do płaszczyzny 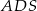ADS ). To pozwala obliczyć długość krawędzi kwadratu w podstawie.

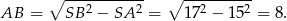
∘ ----------- ∘ ---------- AB = SB 2 − SA 2 = 1 72 − 1 52 = 8.

Wiemy więc jakie są długości podstaw trapezu 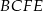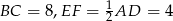BCF E : 1 BC = 8,EF = 2AD = 4 . Potrzebujemy jeszcze jego wysokości. Obliczmy najpierw długość odcinka 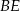BE . Pamiętamy, że 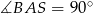∡BAS = 90 ∘ , zatem

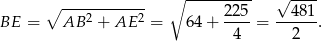
∘ --------- √ ---- ∘ ----2------2 225 481 BE = AB + AE = 64 + -4--= --2--.

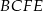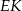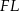Rysujemy teraz z boku trapez BCF E i zaznaczamy jego wysokości EK i F L . Z trójkąta prostokątnego 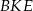BKE mamy

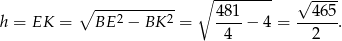
∘ ----------- ∘ 481----- √ 465- h = EK = BE 2 − BK 2 = ----− 4 = ------. 4 2

Pozostało obliczyć pole trapezu

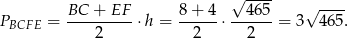
√ ---- √ ---- P = BC--+-EF- ⋅h = 8+--4⋅ --465-= 3 465. BCFE 2 2 2

 
Odpowiedź: √ ---- 3 46 5

Wersja PDF