Zadanie nr 8377230
Pięcioro przyjaciół zamierza na przyjęciu dać sobie nawzajem prezenty w taki sposób, że każdy da tylko jednej osobie prezent, i każdy otrzyma prezent tylko od jednej osoby (oczywiście nikt nie daje prezentu sobie). Na ile sposobów można to zrobić?
A) 5 B) 10 C) 44 D) 50 E) 120
Rozwiązanie
Ustalmy jedną osobę, powiedzmy 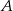 . Może ona dać prezent na 4 sposoby. Niech
. Może ona dać prezent na 4 sposoby. Niech 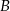 będzie osobą, która otrzymała prezent od
będzie osobą, która otrzymała prezent od 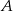 . Mamy teraz dwie istotnie różne sytuacje.
. Mamy teraz dwie istotnie różne sytuacje.
Jeżeli 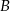 daje prezent
daje prezent 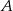 , to
, to 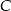 ,
, 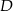 i
i 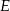 muszą dać sobie prezenty nawzajem – mogą to zrobić na dwa sposoby.
muszą dać sobie prezenty nawzajem – mogą to zrobić na dwa sposoby.
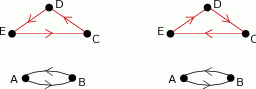
W sumie, w tej sytuacji, mamy 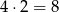 możliwości
możliwości
Jeżeli  nie daje prezentu
nie daje prezentu  , to daje jednej z pozostałych 3 osób. Każdy z tych wyborów jest równoważny, powiedzmy, że
, to daje jednej z pozostałych 3 osób. Każdy z tych wyborów jest równoważny, powiedzmy, że  daje prezent
daje prezent  .
.
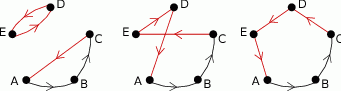
Dalej,  może dać prezent na 3 sposoby i łatwo zobaczyć, że niezależenie od tego, której osobie daje prezent, osoby
może dać prezent na 3 sposoby i łatwo zobaczyć, że niezależenie od tego, której osobie daje prezent, osoby 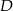 i
i 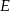 nie mają już żadnego wyboru. Rzeczywiście, jeżeli
nie mają już żadnego wyboru. Rzeczywiście, jeżeli 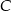 daje prezent
daje prezent 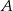 , to
, to 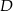 i
i 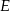 muszą dać prezenty sobie nawzajem. Jeżeli natomiast
muszą dać prezenty sobie nawzajem. Jeżeli natomiast 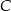 daje prezent np.
daje prezent np. 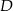 , to
, to 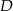 musi dać
musi dać 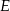 (bo
(bo 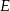 musi od kogoś dostać prezent) i
musi od kogoś dostać prezent) i 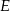 musi dać
musi dać 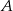 . Podobnie jeżeli
. Podobnie jeżeli 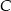 daje prezent
daje prezent 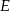 . Mamy więc w tym przypadku
. Mamy więc w tym przypadku 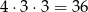 możliwości.
możliwości.
Razem mamy 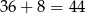 możliwości.
możliwości.
Odpowiedź: C

