Zadanie nr 1886926
Kwadrat o polu 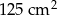 podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta?
podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta?

A) 1 cm B) 1,2 cm C) 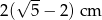 D)
D) 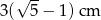 E)
E) 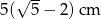
Rozwiązanie
Ponieważ części mają równe pola, to każda ma pole 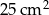 . W szczególności bok małego kwadratu jest równy 5.
. W szczególności bok małego kwadratu jest równy 5.
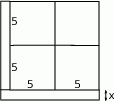
Jeżeli przez  oznaczymy szukaną długość i podzielimy sześciokąt na dwa prostokąty tak jak na rysunku, to mamy równanie
oznaczymy szukaną długość i podzielimy sześciokąt na dwa prostokąty tak jak na rysunku, to mamy równanie
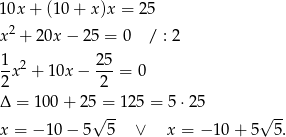
Ujemne rozwiązanie odrzucamy i mamy
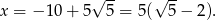
Odpowiedź: E

