Zadanie nr 2107839
Wyznacz największą wartość funkcji
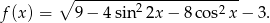
Rozwiązanie
Na początku skorzystajmy ze wzoru
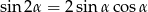
aby pozbyć się 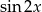 .
.
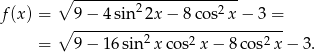
Sposób I
Ponieważ 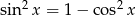 możemy podstawić
możemy podstawić 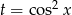 . Wtedy
. Wtedy ![t ∈ [0 ,1]](https://img.zadania.info/zad/2107839/HzadR5x.gif) oraz
oraz
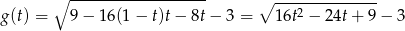
Sprawdźmy jakie są miejsca zerowe trójmianu pod pierwiastkiem
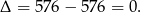
Zatem pod pierwiastkiem jest pełen kwadrat:
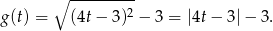
Aby teraz ustalić jaka jest największa wartość tej funkcji na przedziale ![[0,1]](https://img.zadania.info/zad/2107839/HzadR9x.gif) szkicujemy jej wykres – Rozpoczynamy od prostej
szkicujemy jej wykres – Rozpoczynamy od prostej 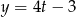 i odbijamy część pod osią
i odbijamy część pod osią 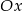 do góry. Potem przesuwamy otrzymany wykres o 3 jednostki w dół.
do góry. Potem przesuwamy otrzymany wykres o 3 jednostki w dół.
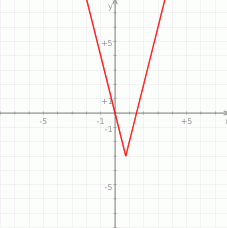
Ze szkicowego rysunku widać, że wartość największa to albo 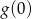 albo
albo 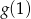 . Która z tych wartości? – liczymy obie i porównujemy
. Która z tych wartości? – liczymy obie i porównujemy
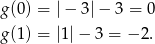
Zatem największa wartość to 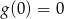 . Nie musimy tego robić, ale możemy zauważyć, że
. Nie musimy tego robić, ale możemy zauważyć, że 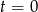 odpowiada takim wartościom
odpowiada takim wartościom  , że
, że 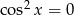 , czyli punktom
, czyli punktom 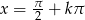 , gdzie
, gdzie 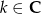 .
.
Sposób II
Jak poprzednio dochodzimy do równości
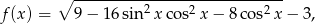
ale teraz podstawmy 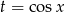 . W szczególności, teraz
. W szczególności, teraz 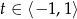 .
.
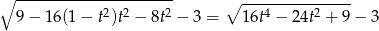
Pod pierwiastkiem mamy funkcję dwukwadratową, więc możemy podstawić 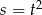 . Wtedy
. Wtedy 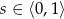 oraz
oraz
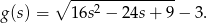
Wartość największą tej funkcji wyznaczamy dokładnie tak samo jak w poprzednim sposobie.
Odpowiedź: