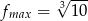/Szkoła średnia/Funkcje/Trygonometryczna/Zbiór wartości

Zadanie nr 4775483

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz największą wartość funkcji 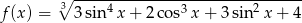3∘ -----4---------3---------2------ f(x ) = 3 sin x + 2 cos x + 3 sin x + 4 .

Rozwiązanie

Ponieważ funkcja 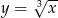√3-- y = x jest rosnąca, wystarczy wyznaczyć największą wartość funkcji

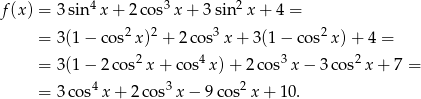
4 3 2 f (x ) = 3sin x+ 2co s x + 3sin x+ 4 = = 3(1 − cos2 x)2 + 2cos3 x+ 3(1− cos2x )+ 4 = = 3(1 − 2 cos2x + cos4 x)+ 2co s3 x − 3co s2x + 7 = 4 3 2 = 3co s x + 2 cos x − 9 cos x + 1 0.

Aby pozbyć się cosinusów, podstawiamy 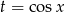t = cos x . Musimy więc wyznaczyć wartość największą funkcji

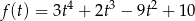
f(t) = 3t4 + 2t3 − 9t2 + 10

na przedziale 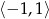⟨− 1,1⟩ (bo takie wartości przyjmuje 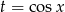t = co sx ). Liczymy pochodną

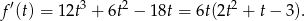
f′(t) = 12t3 + 6t2 − 18t = 6t(2t2 + t− 3).

Rozkładamy jeszcze trójmian w nawiasie.

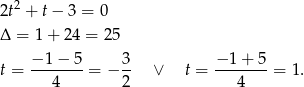
2t2 + t− 3 = 0 Δ = 1 + 24 = 2 5 − 1 − 5 3 − 1+ 5 t = ------- = − -- ∨ t = -------= 1. 4 2 4

Mamy więc

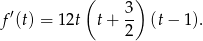
( 3) f′(t) = 12t t+ -- (t− 1). 2

W takim razie pochodna jest dodatnia na przedziale 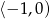⟨− 1,0) i ujemna na przedziale 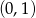(0 ,1) , czyli funkcja 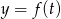y = f(t) rośnie w pierwszym z tych przedziałów i maleje w drugim.

PIC

To oznacza, że największą wartością tej funkcji jest

f(0) = 10 .

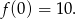
Największa wartość funkcji danej w treści zadania to 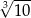√ --- 31 0 .

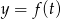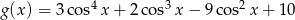Na koniec dla ciekawskich wykresy funkcji y = f(t) i g (x ) = 3co s4x + 2 cos3x − 9 cos2x + 10 .

PIC

 
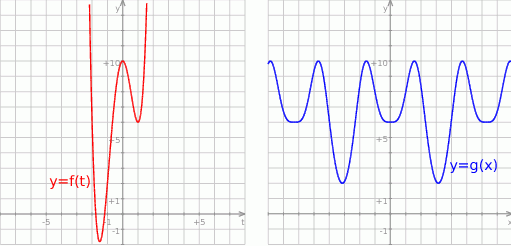
Odpowiedź: √ --- fmax = 3 10

Wersja PDF