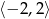Zadanie nr 4924981
Wyznacz zbiór wartości funkcji
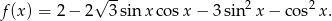
Rozwiązanie
Sposób I
Przekształćmy najpierw podany wzór funkcji. Będziemy korzystać ze wzorów
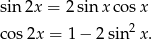
Aby móc skorzystać z drugiego z tych wzorów, zamienimy 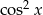 na
na 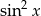 (z jedynki trygonometrycznej).
(z jedynki trygonometrycznej).
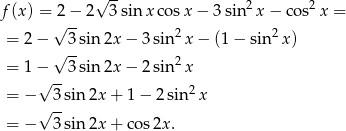
Przekształcimy dalej otrzymany wzór, korzystając z tożsamości
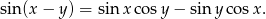
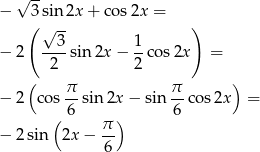
Widać teraz, że zbiór wartości danej funkcji, to przedział 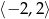 .
.
Sposób II
Tak jak w poprzednim sposobie sprowadzamy funkcję do postaci
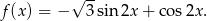
Aby znaleźć zbiór wartości funkcji 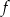 , zbadamy jej minima i maksima. W tym celu liczymy pochodną
, zbadamy jej minima i maksima. W tym celu liczymy pochodną
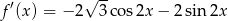
i szukamy jej miejsc zerowych. Pochodna nie jest równa 0 dla 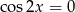 , więc możemy założyć, że
, więc możemy założyć, że 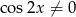 .
.
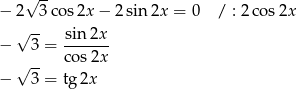
Widzimy więc, że miejsca zerowe pochodnej są w punktach 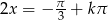 . Aby ustalić, gdzie są minima a gdzie maksima, musimy zbadać znak pochodnej. W tym celu zapiszmy ją w postaci
. Aby ustalić, gdzie są minima a gdzie maksima, musimy zbadać znak pochodnej. W tym celu zapiszmy ją w postaci
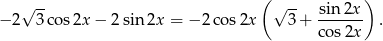
Można teraz sprawdzić, że jeżeli 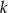 jest parzyste to jest maksimum, a gdy
jest parzyste to jest maksimum, a gdy 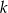 jest nieparzyste to jest minimum. Odpowiadające wartości
jest nieparzyste to jest minimum. Odpowiadające wartości 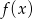 , to
, to
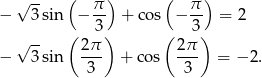
Sposób III
Tym razem odrobinę inaczej przekształcimy wzór funkcji
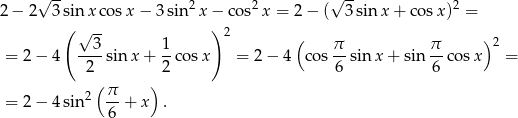
Ponieważ 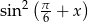 przyjmuje wartości z przedziału
przyjmuje wartości z przedziału 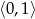 , funkcja
, funkcja 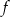 przyjmuje wartości z przedziału
przyjmuje wartości z przedziału 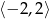 .
.
Odpowiedź: