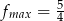/Szkoła średnia/Funkcje/Trygonometryczna/Zbiór wartości

Zadanie nr 7397446

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 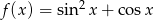2 f(x ) = sin x + cos x dla x ∈ R .

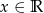  • Rozwiąż równanie 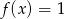f (x) = 1 w przedziale ⟨0,2π⟩ .
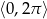  • Wyznacz największą wartość funkcji f .

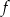Rozwiązanie

Przekształćmy najpierw wzór funkcji:

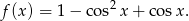
2 f(x ) = 1− cos x + co sx.
  • Uwzględniając powyższe przekształcenie, mamy
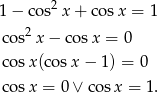
    1− cos2x + cos x = 1 2 cos x− cosx = 0 cos x(cosx − 1) = 0 cos x = 0 ∨ cosx = 1.

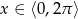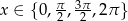    Uwzględniając, że x ∈ ⟨0,2π ⟩ , dostajemy x ∈ {0, π, 3π-,2 π} 2 2 .  
    Odpowiedź: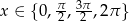 π- 3π- x ∈ {0, 2, 2 ,2π }

  • Jeżeli podstawimy 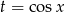t = cos x to mamy zwykłą parabolę 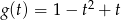g(t) = 1− t2 + t na przedziale 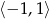⟨− 1,1⟩ (bo takie wartości przyjmuje 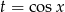t = co sx na podanym przedziale) – rysunek.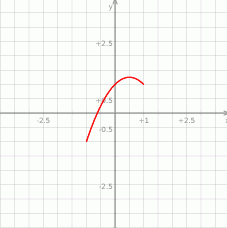
    PIC

    Łatwo obliczyć, że wierzchołek tej paraboli ma współrzędne 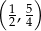( ) 1 5 2 ,4 . Ponieważ 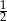1 2 znajduje się wewnątrz przedziału 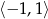⟨− 1,1⟩ , funkcja 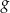g przyjmuje największą wartość w punkcie 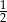1 2 i wynosi ona 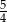5 4 . Oczywiście jest to też największa wartość funkcji f .  
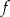    Odpowiedź: fmax = 54

Wersja PDF