Zadanie nr 9308644
Wyznacz zbiór wartości funkcji
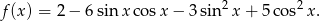
Rozwiązanie
Przekształćmy najpierw podany wzór funkcji. Będziemy korzystać ze wzorów
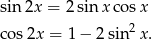
Aby móc skorzystać z drugiego z tych wzorów, zamienimy 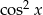 na
na 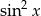 (z jedynki trygonometrycznej).
(z jedynki trygonometrycznej).
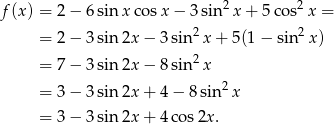
Sposób I
Przekształcimy dalej otrzymany wzór, korzystając z tożsamości
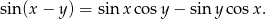
Aby zastosować ten wzór, dobierzemy współczynniki przy 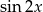 i
i 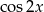 tak aby ich suma kwadratów była równa 1. Dzięki temu będziemy je mogli napisać jako
tak aby ich suma kwadratów była równa 1. Dzięki temu będziemy je mogli napisać jako 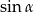 i
i 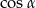 dla pewnego
dla pewnego  .
.
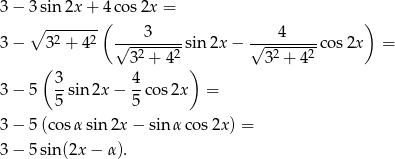
Widać teraz, że zbiór wartości danej funkcji, to przedział 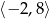 .
.
Sposób II
Aby znaleźć zbiór wartości funkcji 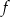 , zbadamy jej minima i maksima. W tym celu liczymy pochodną
, zbadamy jej minima i maksima. W tym celu liczymy pochodną
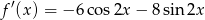
i szukamy jej miejsc zerowych. Pochodna nie jest równa 0 dla 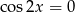 , więc możemy założyć, że
, więc możemy założyć, że 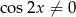 .
.
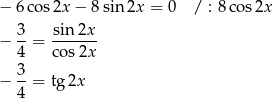
Widzimy więc, że miejsca zerowe pochodnej są w takich punktach, że 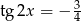 . Tak naprawdę nie musimy ustalać gdzie są minima, a gdzie maksima – to się samo okaże, gdy będziemy liczyć wartości funkcji w tych punktach.
. Tak naprawdę nie musimy ustalać gdzie są minima, a gdzie maksima – to się samo okaże, gdy będziemy liczyć wartości funkcji w tych punktach.
Żeby te wartości policzyć, musimy wyliczyć 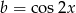 i
i 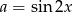 , wiedząc, że
, wiedząc, że 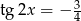 . Mamy układ równań:
. Mamy układ równań:
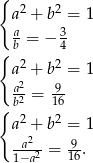
Prowadzi to do równania
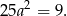
Ponieważ iloraz 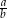 ma być ujemny, prowadzi to do dwóch par rozwiązań
ma być ujemny, prowadzi to do dwóch par rozwiązań
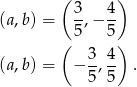
Pierwsze z rozwiązań daje nam wartość najmniejszą naszej funkcji, a drugie wartość największą.
Odpowiedź: