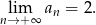Zadanie nr 3799707
Wykazać zbieżność ciągu określonego rekurencyjnie: 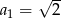 ,
, 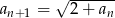 dla
dla 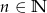 i wyznaczyć jego granicę.
i wyznaczyć jego granicę.
Rozwiązanie
Aby wykazać, że ciąg jest zbieżny wystarczy pokazać, że jest on monotoniczny i ograniczony. Bawiąc się chwilę kalkulatorem można zgadnąć, że podany ciąg jest rosnący i ograniczony z góry przez 2. Spróbujmy to uzasadnić.
Jeżeli założymy indukcyjnie, że 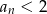 to mamy
to mamy
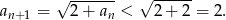
Spróbujmy teraz pokazać, że ciąg jest rosnący.
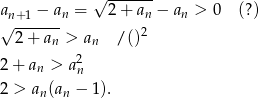
Ponieważ pokazaliśmy już, że 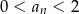 powyższa nierówność jest spełniona, czyli ciąg jest rosnący.
powyższa nierówność jest spełniona, czyli ciąg jest rosnący.
Skoro wiemy, że ciąg jest zbieżny, oznaczmy jego granicę przez 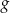 i przejdźmy do granicy po obu stronach równości
i przejdźmy do granicy po obu stronach równości
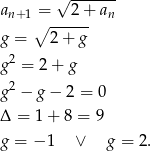
Oczywiście ujemne rozwiązanie odrzucamy i mamy