/Studia/Analiza/Ciągi/Granice

Zadanie nr 9996170

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że nie istnieje granica 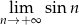nl→im+∞ sin n .

Rozwiązanie

Sposób I

Załóżmy, że granica istnieje i oznaczmy

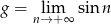
g = nl→im+∞ sinn

Korzystając ze wzoru na sinus podwojonego kąta mamy

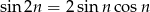
sin 2n = 2sin nco sn

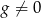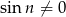Jeżeli g ⁄= 0 , to sin n ⁄= 0 dla dostatecznie dużych n i mamy

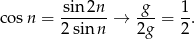
sin-2n- -g- 1- cosn = 2sin n → 2g = 2 .

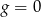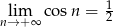Zatem albo g = 0 albo lim co sn = 1 n→ + ∞ 2 . Ta druga możliwość łatwo jednak prowadzi do sprzeczności ze wzorem

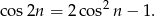
co s2n = 2cos2 n− 1.

Zatem 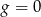g = 0 i korzystając ze wzoru na sinus sumy mamy

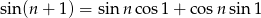
sin(n + 1) = sin nc os1 + cos nsin 1

Ponieważ pierwsze dwa z powyższych ciągów są zbieżne, więc zbieżny jest także ciąg 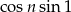co sn sin 1 i jego granica wynosi

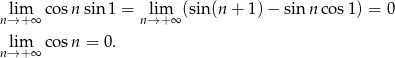
lim co sn sin 1 = lim (sin(n + 1) − sinn cos 1) = 0 n→ +∞ n→ + ∞ lim co sn = 0 . n→ +∞

Z drugiej strony, ponieważ

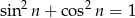
sin 2n + cos2 n = 1

Więc przechodząc w tej równości do granicy otrzymujemy 0=1, co jest oczywiście niemożliwe.

Sposób II

Tym razem wprost wskażemy dwa podciągi danego ciągu, które nie mogą być zbieżne do tej samej granicy. Wiemy, że

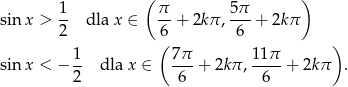
1 ( π 5π ) sin x > -- dla x ∈ --+ 2kπ ,---+ 2kπ 2 6( 6 ) 1- 7π- 11π- sin x < − 2 dla x ∈ 6 + 2kπ , 6 + 2kπ .

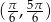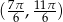Ponieważ każdy z przedziałów π- 5π- (6 , 6 ) i 7π- 11π ( 6 , 6 ) ma długość

4π --- > 2, 6

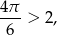
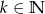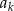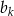więc dla każdego k ∈ N , możemy znaleźć liczby naturalne a k i b k dla których

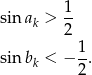
1 sin ak > -- 2 sin bk < − 1. 2

W ten sposób mam dwa podciągi ciągu 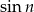sin n , które nie mogą być zbieżne do tej samej granicy.

Wersja PDF