Zadanie nr 4568702
Końce cięciwy 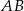 okręgu o równaniu
okręgu o równaniu 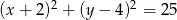 leżą na prostej
leżą na prostej 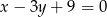 . Oblicz sinus kąta wypukłego
. Oblicz sinus kąta wypukłego 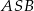 , gdzie
, gdzie 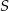 jest środkiem danego okręgu.
jest środkiem danego okręgu.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
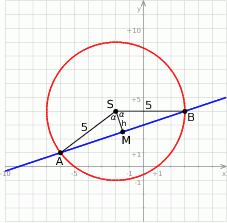
Na początek wyznaczmy współrzędne punktów 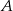 i
i 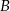 – podstawiamy
– podstawiamy 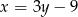 do równania okręgu.
do równania okręgu.
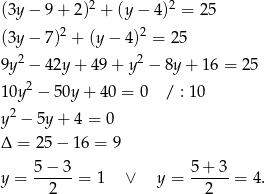
Mamy wtedy odpowiednio 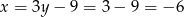 i
i 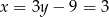 . Zatem
. Zatem 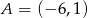 i
i 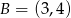 .
.
Sposób I
Obliczmy pole trójkąta 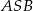 (żeby ze wzoru na pole z sinusem wyliczyć
(żeby ze wzoru na pole z sinusem wyliczyć 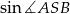 ). Jego podstawa ma długość
). Jego podstawa ma długość
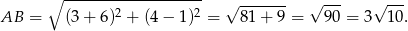
Wysokość opuszczona na tę podstawę to odległość punktu 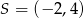 od prostej
od prostej 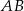 , czyli
, czyli
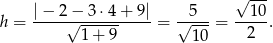
Zatem pole trójkąta jest równe
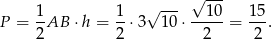
Teraz korzystamy ze wzoru na pole z sinusem.
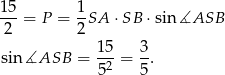
Sposób II
Tak jak w poprzednim sposobie obliczamy odległość punktu 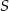 od prostej
od prostej 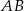 .
.
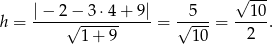
Mamy zatem
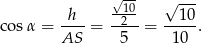
Stąd
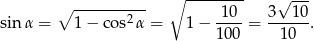
Teraz pozostało skorzystać ze wzoru na 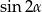 .
.
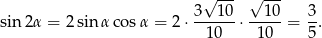
Zauważmy, że w tym sposobie nie były nam potrzebne współrzędne punktów 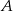 i
i 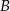 .
.
Sposób III
Pole trójkąta 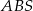 możemy obliczyć ze wzoru na pole trójkąta o wierzchołkach
możemy obliczyć ze wzoru na pole trójkąta o wierzchołkach 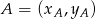 ,
, 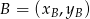 i
i 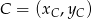 .
.
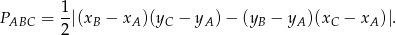
W naszej sytuacji mamy
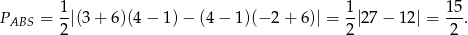
Sinus obliczamy jak w poprzednim sposobie.
Sposób IV
Liczymy długość odcinka 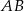
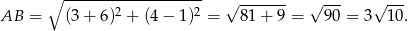
Jeżeli więc przez 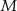 oznaczymy środek odcinka
oznaczymy środek odcinka 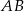 to
to 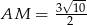 . Dorysujmy wysokość
. Dorysujmy wysokość 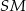 i oznaczmy
i oznaczmy 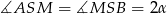 . Na mocy twierdzenia Pitagorasa w trójkącie
. Na mocy twierdzenia Pitagorasa w trójkącie 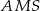 mamy
mamy
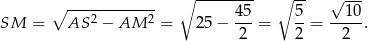
Mamy więc
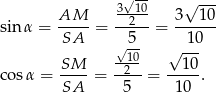
Teraz pozostało skorzystać ze wzoru na 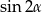 .
.
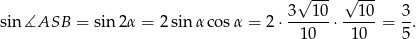
Sposób V
Liczymy długość odcinka 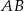
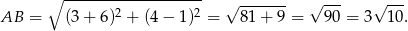
Teraz korzystamy z twierdzenia cosinusów.
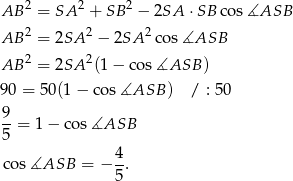
Zatem
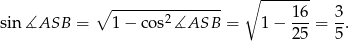
Odpowiedź: