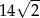/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Punkty wspólne z prostą

Zadanie nr 5320913

Oblicz długość cięciwy, którą wycina z prostej 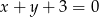x + y+ 3 = 0 okrąg o środku w punkcie 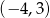(− 4,3) i promieniu 10.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

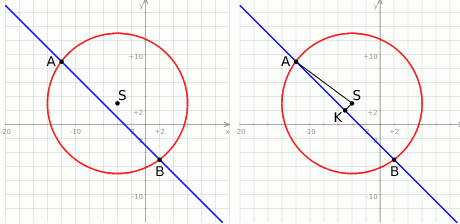
Sposób I

Równanie okręgu, o którym mowa w treści zadania ma postać

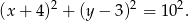
(x + 4)2 + (y − 3)2 = 102.

Aby wyznaczyć jego punkty wspólne z podaną prostą podstawiamy w powyższym równaniu 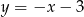y = −x − 3 .

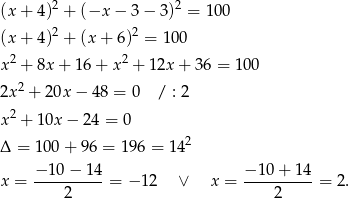
(x + 4)2 + (−x − 3 − 3)2 = 100 2 2 (x + 4) + (x + 6) = 10 0 x2 + 8x + 16 + x 2 + 1 2x+ 36 = 10 0 2x 2 + 20x − 48 = 0 / : 2 2 x + 10x − 2 4 = 0 Δ = 100 + 96 = 196 = 142 x = −-10−--14-= − 1 2 ∨ x = −-10-+-1-4 = 2. 2 2

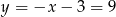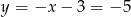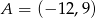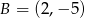Mamy wtedy odpowiednio y = −x − 3 = 9 i y = −x − 3 = − 5 . Zatem końce interesującej nas cięciwy to A = (− 12,9) i B = (2,− 5) . Pozostało obliczyć długość odcinka AB .

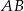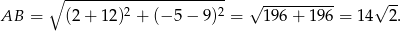
∘ ---------------------- √ ---------- √ -- AB = (2 + 12 )2 + (− 5 − 9)2 = 1 96+ 196 = 14 2.

Sposób II

Jeżeli przez 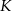K oznaczmy środek cięciwy 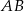AB to trójkąt 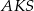AKS jest prostokątny i wystarczy obliczyć długość przyprostokątnej 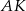AK . Wiemy, że 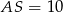AS = 10 , a długość odcinka 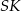SK to odległość punktu 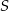S od prostej 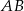AB . Zatem

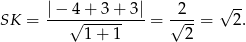
|−-4-+-3-+-3|- -2-- √ -- SK = √ ------ = √ --= 2. 1+ 1 2

Mamy więc

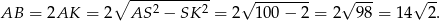
∘ ---2-----2- √ -------- √ --- √ -- AB = 2AK = 2 AS − SK = 2 100 − 2 = 2 98 = 14 2.

 
Odpowiedź: √ -- 14 2

Wersja PDF