Zadanie nr 5591448
Punkty 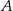 i
i 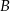 są punktami wspólnymi prostej o równaniu
są punktami wspólnymi prostej o równaniu 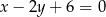 oraz okręgu o środku
oraz okręgu o środku 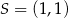 . Długość odcinka
. Długość odcinka 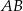 jest równa
jest równa 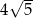 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 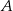 i
i 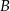 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
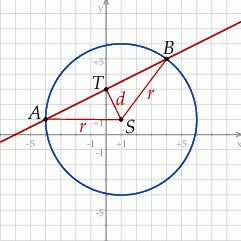
Zauważmy, że z trójkąta prostokątnego 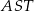 dość łatwo możemy wyznaczyć długość promienia
dość łatwo możemy wyznaczyć długość promienia  okręgu, o którym mowa w treści zadania. Zanim to jednak zrobimy, obliczmy odległość
okręgu, o którym mowa w treści zadania. Zanim to jednak zrobimy, obliczmy odległość 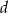 punktu
punktu 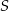 od danej prostej
od danej prostej
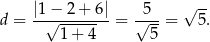
Piszemy teraz twierdzenie Pitagorasa w trójkącie 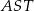 .
.
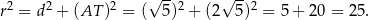
Zatem 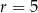 i dany okrąg ma równanie
i dany okrąg ma równanie
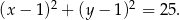
Szukamy teraz punktów 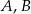 wspólnych tego okręgu i danej prostej. Podstawiamy
wspólnych tego okręgu i danej prostej. Podstawiamy 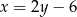 do równania okręgu.
do równania okręgu.
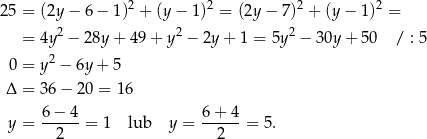
Mamy wtedy 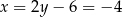 i
i 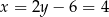 odpowiednio. Punkty
odpowiednio. Punkty 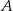 i
i 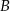 mają więc współrzędne (niekoniecznie w tej kolejności):
mają więc współrzędne (niekoniecznie w tej kolejności): 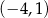 i
i 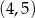 .
.
Odpowiedź: 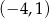 i
i