Zadanie nr 7371486
Prosta o równaniu 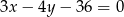 przecina okrąg o środku
przecina okrąg o środku 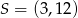 w punktach
w punktach 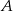 i
i 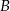 . Długość odcinka
. Długość odcinka 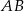 jest równa 40. Wyznacz równanie tego okręgu.
jest równa 40. Wyznacz równanie tego okręgu.
Rozwiązanie
Zacznijmy od rysunku i oznaczmy rzut punktu 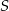 na daną prostą przez
na daną prostą przez 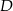 .
.
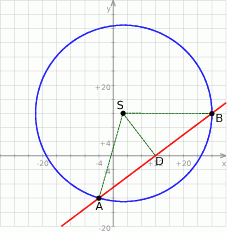
To co musimy obliczyć, to promień  szukanego okręgu. Obliczymy go z trójkąta prostokątnego
szukanego okręgu. Obliczymy go z trójkąta prostokątnego 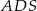 . Jedna z jego przyprostokątnych to połowa cięciwy
. Jedna z jego przyprostokątnych to połowa cięciwy 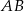 , a druga to odległość punktu
, a druga to odległość punktu 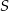 od danej prostej.
od danej prostej.
Korzystamy ze wzoru na odległość punktu 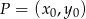 od prostej
od prostej 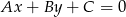 :
:
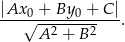
W naszej sytuacji mamy
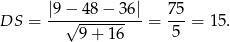
Stosując twierdzenie Pitagorasa do trójkąta 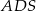 mamy
mamy
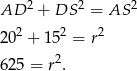
Teraz, bez problemu piszemy równanie poszukiwanego okręgu
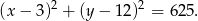
Odpowiedź: