/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Punkty wspólne z prostą

Zadanie nr 8792177

Wyznacz wszystkie wartości parametru 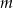m , dla których okrąg o równaniu 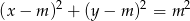(x − m )2 + (y− m )2 = m 2 jest styczny do prostej y = −x + 3 .

Wersja PDF

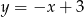Rozwiązanie

Szkicujemy opisaną sytuację

PIC

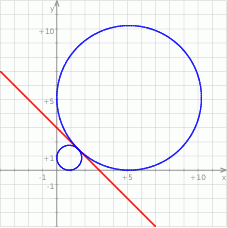
Sposób I

Podstawiamy 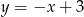y = −x + 3 w danym równaniu okręgu.

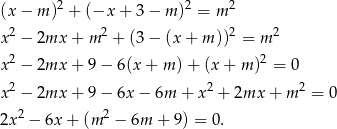
2 2 2 (x − m ) + (−x + 3 − m ) = m x2 − 2mx + m 2 + (3− (x + m ))2 = m 2 2 2 x − 2mx + 9 − 6(x + m )+ (x+ m ) = 0 x2 − 2mx + 9 − 6x − 6m + x2 + 2mx + m 2 = 0 2x2 − 6x + (m 2 − 6m + 9) = 0.

Jeżeli okrąg ma być styczny do prostej, to powyższe równanie musi mieć dokładnie jedno rozwiązanie, czyli

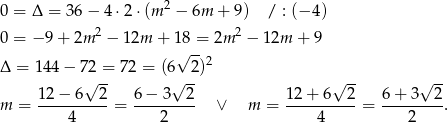
0 = Δ = 3 6− 4⋅2 ⋅(m 2 − 6m + 9 ) / : (− 4) 2 2 0 = − 9+ 2m − 12m + 18 = 2m − 12m + 9 √ -- 2 Δ = 144 − 72√ =- 72 = (6√ 2-) √ -- √ -- 12− 6 2 6− 3 2 1 2+ 6 2 6+ 3 2 m = ----------= --------- ∨ m = ---------- = --------. 4 2 4 2

Sposób II

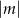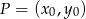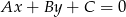Jeżeli prosta ma być styczna do okręgu, to środek tego okręgu musi być odległy od tej prostej o długość promienia, czyli o |m| . Korzystając ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

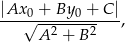
|Ax-0√-+-By-0 +-C|, A 2 + B 2

mamy w naszej sytuacji równanie

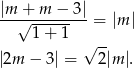
|m√+-m-−--3| 1 + 1 = |m | √ -- |2m − 3| = 2|m |.

Ponieważ obie strony równania są nieujemne, możemy je podnieść stronami do kwadratu i mamy

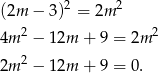
(2m − 3)2 = 2m 2 2 2 4m − 12m + 9 = 2m 2m 2 − 12m + 9 = 0.

Równanie rozwiązujemy tak samo jak w poprzednim sposobie.  
Odpowiedź: 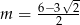√- m = 6−-32-2 lub √ - m = 6+32--2

Wersja PDF