/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Punkty wspólne z prostą

Zadanie nr 9540592

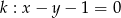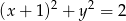Określ wzajemne położenie prostej k : x − y − 1 = 0 i okręgu o równaniu (x + 1)2 + y2 = 2 .

Wersja PDF

Rozwiązanie

Możemy zacząć od szkicowego rysunku.

PIC

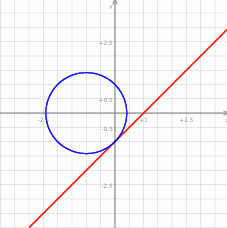
Sposób I

Sprawdzamy ile punktów wspólnych mają podany okrąg i prosta – wstawiamy 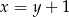x = y+ 1 z równania prostej do równania okręgu.

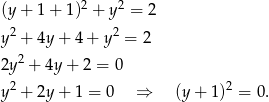
2 2 (y+ 1+ 1) + y = 2 y2 + 4y+ 4+ y2 = 2 2 2y + 4y + 2 = 0 2 2 y + 2y+ 1 = 0 ⇒ (y + 1) = 0.

Równanie to ma jedno rozwiązanie, więc podane prosta i okrąg są styczne.

Sposób II

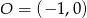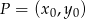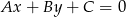Zamiast szukać punktów wspólnych podanych krzywych, sprawdźmy jaka jest odległość środka okręgu O = (− 1,0) od danej prostej. Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

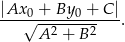
|Ax-0√-+-By-0 +-C|. A 2 + B 2

W naszej sytuacji mamy

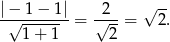
|-−√-1-−-1| = √2--= √ 2. 1+ 1 2

Ponieważ ta odległość jest dokładnie równa promieniowi danego okręgu, krzywe te są styczne.  
Odpowiedź: Są styczne.

Wersja PDF