/Konkursy/Zadania testowe/Liczby/Oś liczbowa

Zadanie nr 1032033

Dodaj do ulubionych
Dodaj do rozwiązanych

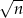Ile jest liczb całkowitych dodatnich n takich, że odległość na osi liczbowej między liczbami √ -- n i 10 jest mniejsza niż 1.
A) 19 B) 20 C) 38 D) 39 E) 40

Rozwiązanie

Sposób I

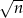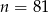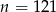Dla jakich liczb odległość √ -- n od 10 jest równa dokładnie 1? – dla n = 81 i n = 121 . Interesują nas zatem liczby od 82 do 120. Ponieważ

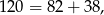
120 = 82 + 3 8,

tych liczb jest 39 (tyle ile liczb od 0 do 38).

Sposób II

Pytanie brzmi ile jest liczb dla których

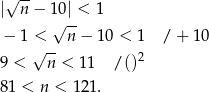
|√n--− 1 0| < 1 √ -- − 1 < n − 10 < 1 / + 10 √ -- 2 9 < n < 1 1 /() 81 < n < 121.

Ilość tych liczb liczymy jak poprzednio.  
Odpowiedź: D

Wersja PDF