/Szkoła średnia/Ciągi/Rekurencyjny

Zadanie nr 2758163

Dany jest ciąg 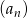(an) określony dla każdej liczby całkowitej 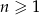n ≥ 1 , w którym dla każdej liczby 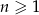n ≥ 1 prawdziwe są równości

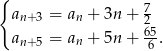
{ an+3 = an + 3n + 72 a = an + 5n + 65. n+5 6

Wykaż, że ciąg 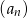(an ) jest ciągiem rosnącym.

Wersja PDF

Rozwiązanie

Sposób I

Zastanówmy się najpierw w jaki sposób podane warunki wyznaczają kolejne wyrazy ciągu 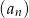(an ) . Jeżeli znamy 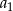a1 , to pierwszy warunek pozwala obliczyć 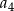a4 . Jeżeli teraz podstawimy 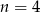n = 4 w pierwszym warunku, to z 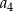a 4 otrzymamy 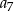a 7 . Po podstawieniu 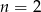n = 2 w drugim warunku obliczymy 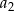a2 . W ten pokrętny sposób udało nam się obliczyć 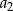a2 jeżeli znamy a1 .

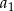Spróbujmy wykonać teraz te same operacje, ale w ogólnej sytuacji. Podstawmy w pierwszej z podanych równości 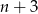n+ 3 zamiast n . Otrzymujemy wtedy

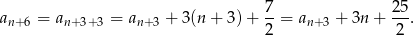
7- 25- an+6 = an+ 3+3 = an+ 3 + 3(n+ 3)+ 2 = an +3 + 3n + 2 .

W połączeniu z pierwszą równością mamy zatem

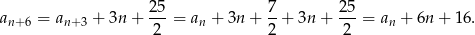
a = a + 3n + 25-= a + 3n+ 7-+ 3n + 25-= a + 6n + 16. n+6 n+ 3 2 n 2 2 n

Podstawiamy teraz 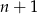n + 1 w drugim warunku i korzystamy z powyższej równości.

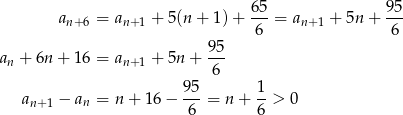
65 95 an+ 6 = an+ 1 + 5(n + 1)+ ---= an+ 1 + 5n + --- 6 6 an + 6n + 16 = a + 5n + 95- n+ 1 6 9-5 1- an+ 1 − an = n + 16 − 6 = n + 6 > 0

co oczywiście oznacza, że ciąg 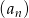(an) jest rosnący.

Sposób II

Podstawmy w pierwszej z podanych równości 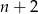n+ 2 zamiast n . Otrzymujemy wtedy

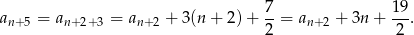
7 19 an+5 = an+ 2+3 = an+ 2 + 3(n+ 2)+ --= an +2 + 3n + ---. 2 2

W połączeniu z drugą równością mamy zatem

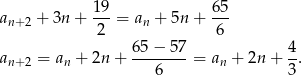
19- 65- an+ 2 + 3n+ 2 = an + 5n + 6 6 5− 57 4 an+ 2 = an + 2n + -------- = an + 2n + -. 6 3

Podstawmy teraz w tym warunku 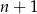n + 1 zamiast n .

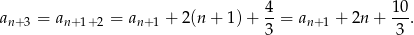
4 10 an+3 = an+ 1+2 = an+ 1 + 2(n+ 1)+ --= an +1 + 2n + ---. 3 3

Porównujemy teraz ten warunek z pierwszą równością z treści zadania.

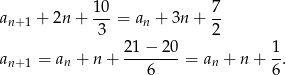
10 7 an +1 + 2n + -3-= an + 3n + 2- an +1 = an + n + 2-1−--20 = an + n + 1. 6 6

W takim razie

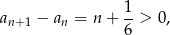
1 an+ 1 − an = n + --> 0, 6

co oczywiście oznacza, że ciąg 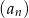(an) jest rosnący.

Wersja PDF