/Szkoła średnia/Ciągi/Rekurencyjny

Zadanie nr 3852248

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ciąg 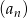(an) określony dla każdej liczby całkowitej 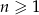n ≥ 1 , w którym 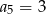a5 = 3 oraz dla każdej liczby 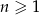n ≥ 1 prawdziwa jest równość 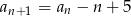an+ 1 = an − n + 5 . Oblicz pierwszy wyraz ciągu 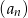(an ) i ustal, czy ciąg ten jest rosnący.

Rozwiązanie

Jeżeli zapiszemy daną zależność rekurencyjną w postaci

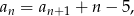
an = an+ 1 + n − 5 ,

to widać jak obliczyć pierwsze wyrazy ciągu 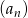(an) .

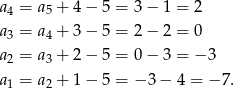
a4 = a5 + 4 − 5 = 3 − 1 = 2 a3 = a4 + 3 − 5 = 2 − 2 = 0 a2 = a3 + 2 − 5 = 0 − 3 = −3 a1 = a2 + 1 − 5 = − 3 − 4 = − 7.

Jeżeli natomiast zapiszemy daną rekurencję w postaci

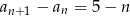
an+ 1 − an = 5− n

to widać, że ciąg nie jest rosnący, bo np.

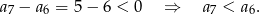
a7 − a6 = 5 − 6 < 0 ⇒ a7 < a6.

 
Odpowiedź: 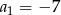a1 = − 7 , nie jest rosnący.

Wersja PDF