Zadanie nr 4756952
Oblicz sumę 50 początkowych wyrazów ciągu 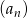 , który określony jest w następujący sposób
, który określony jest w następujący sposób
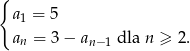
Rozwiązanie
Sposób I
Zauważmy, że
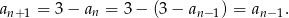
To oznacza, że
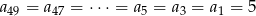
oraz
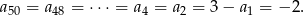
Stąd
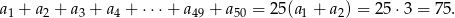
Sposób II
Zauważmy, że z podanej rekurencji mamy 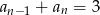 , czyli
, czyli
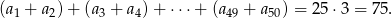
Odpowiedź: 75
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz sumę 50 początkowych wyrazów ciągu 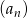 , który określony jest w następujący sposób
, który określony jest w następujący sposób
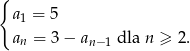
Sposób I
Zauważmy, że
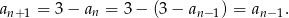
To oznacza, że
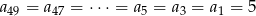
oraz
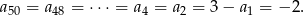
Stąd
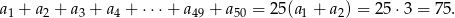
Sposób II
Zauważmy, że z podanej rekurencji mamy 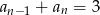 , czyli
, czyli
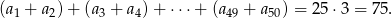
Odpowiedź: 75
