/Szkoła średnia/Ciągi/Rekurencyjny

Zadanie nr 5276279

Dodaj do ulubionych
Dodaj do rozwiązanych

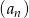Ciąg (an ) określony dla 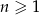n ≥ 1 jest rosnący, ma wszystkie wyrazy ujemne oraz spełnia warunki

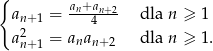
{ a +a an+ 1 = -n-4n+2 dla n ≥ 1 a2 = ana dla n ≥ 1. n+ 1 n+ 2

Oblicz iloraz 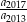a2017- a2013 .

Rozwiązanie

Drugi z podanych warunków możemy zapisać w postaci

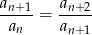
an+1- an+2- a = a n n+1

co oznacza, że mamy do czynienia z ciągiem geometrycznym (ilorazy kolejnych wyrazów są stałe). W takim razie 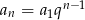n− 1 an = a1q , gdzie przez 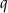q oznaczyliśmy iloraz tego ciągu. Pierwszy warunek możemy więc zapisać w postaci

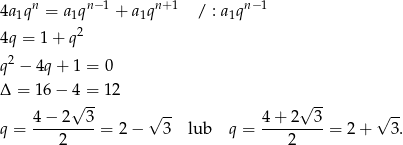
4a 1qn = a1qn− 1 + a1qn +1 / : a1qn−1 2 4q = 1+ q q 2 − 4q + 1 = 0 Δ = 16 − 4√ =- 12 √ -- 4 − 2 3 √ -- 4 + 2 3 √ -- q = ---------= 2− 3 lub q = ---------= 2+ 3. 2 2

Ponieważ wszystkie wyrazy ciągu 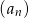(an) są ujemne i jest on rosnący, to musimy mieć 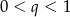0 < q < 1 , więc 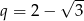√ -- q = 2− 3 . Interesujący nas iloraz jest więc równy

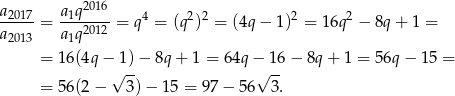
2016 a2017 a1q---- 4 2 2 2 2 a2013 = a1q2012 = q = (q ) = (4q− 1) = 16q − 8q + 1 = = 16(4q −√1)-− 8q + 1 = 64q−√ 16− 8q + 1 = 56q − 1 5 = = 56(2 − 3) − 15 = 97− 56 3.

 
Odpowiedź: √ -- 97 − 56 3

Wersja PDF