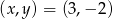Zadanie nr 5276662
Dany jest ciąg określony rekurencyjnie
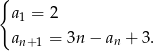
Wyznacz liczby całkowite 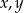 tak, aby ciąg
tak, aby ciąg 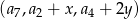 był ciągiem arytmetycznym, natomiast ciąg
był ciągiem arytmetycznym, natomiast ciąg 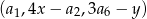 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Rozwiązanie
Obliczmy kilka kolejnych wyrazów ciągu 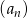 .
.
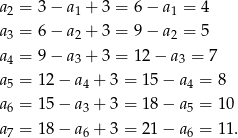
Pytanie zatem brzmi: kiedy ciąg 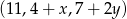 jest arytmetyczny, i kiedy ciąg
jest arytmetyczny, i kiedy ciąg 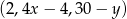 jest geometryczny. Mamy zatem układ równań
jest geometryczny. Mamy zatem układ równań
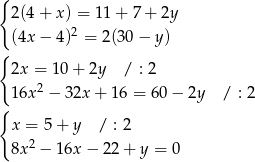
Podstawiamy teraz 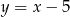 z pierwszego równania do drugiego.
z pierwszego równania do drugiego.
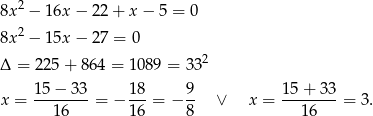
Ponieważ  ma być liczbą całkowitą, mamy
ma być liczbą całkowitą, mamy 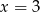 . Stąd
. Stąd 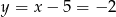 .
.
Odpowiedź: