Zadanie nr 5460756

Ciąg 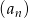(an) , gdzie 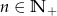n ∈ N + , określony jest następująco:

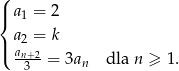
( |{ a1 = 2 a2 = k |( an+2 3 = 3an dla n ≥ 1.

Wyznacz wartość 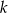, jeżeli ciąg 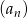jest ciągiem geometrycznym, w którym suma sześciu początkowych wyrazów jest równa .
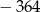Oblicz, dla jakiej liczby suma początkowych wyrazów ciągu 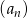jest równa 9842.

Rozwiązanie

Jeżeli ciąg 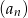ma być geometryczny, to 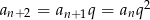, gdzie przez 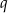oznaczyliśmy jego iloraz. Mamy wtedy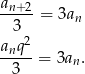
$an+2-= 3a 3 n a q2 -n---= 3an. 3$

Ponieważ 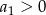, żaden wyraz ciągu 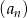nie może być równy 0, więc mamy stąd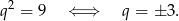

$2 q = 9 ⇐ ⇒ q = ± 3.$

Zauważmy teraz, że dla 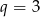otrzymujemy ciąg o wyrazach dodatnich, w którym suma wyrazów nie może być liczbą ujemną. Zatem 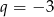i wtedy 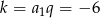. Wtedy rzeczywiście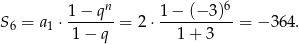

$n 6 1-−-q-- 1−--(−-3)- S6 = a 1 ⋅ 1− q = 2⋅ 1 + 3 = − 364 .$

Odpowiedź: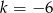
Musimy rozwiązać równanie
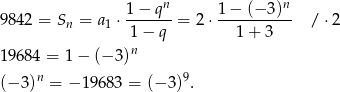
$n n 98 42 = S = a ⋅ 1−-q---= 2 ⋅ 1-−-(−-3)- / ⋅2 n 1 1 − q 1+ 3 n 19 684 = 1 − (− 3) (− 3)n = − 19683 = (− 3)9.$

Zatem .
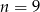Odpowiedź: